How to Solve Triangles Problems? (+FREE Worksheet!)
Learn how to solve mathematics problems related to triangle area and angles using common triangle formulas.
Related Topics
- How Calculate the Area of Trapezoids
- How to Find the volume and surface area of Rectangular Prisms
- How to Find the Area and Circumference of Circles
- How to Find Volume and Surface Area of Cubes
- How to Find the Perimeter of Polygons
A step-by-step guide to solving Triangles
- In any triangle, the sum of all angles is \(180\) degrees.
- Area of a triangle \(= \color{blue}{\frac{1}{2 }(base \ × \ height)}\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Triangles – Example 1:
What is the area of the following triangle?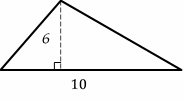 
Solution:
Use the area formula: Area \(= \color{blue}{\frac{1}{2 }(base \ × \ height)}\)
base \(=10\) and height \(=6\)
Area \(= \frac{1}{2} (10×6)=\frac{1}{2} (60)=30\)
Triangles – Example 2:
What is the missing angle of the following triangle?
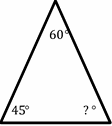
Solution:
All angles in a triangle sum up to \(180\) degrees. Then: : \(45+60+x=180 → 105+x=180 → x=180-105=75\)
Triangles – Example 3:
What is the area of the following triangle?
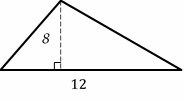
Solution:
Use the area formula: Area \(= \color{blue}{\frac{1}{2 }(base \ × \ height)}\)
base \(=12\) and height \(=8\)
Area \(= \frac{1}{2} (12×8)= \frac{1}{2} (96)=48 \)
The Best Book to Help You Ace Pre-Algebra
Triangles – Example 4:
What is the area of a triangle with base \(6\) and height \(5\)?
Solution:
Use the area formula: Area \(= \color{blue}{\frac{1}{2 }(base \ × \ height)}\)
base \(=6\) and height \(=5\)
Area \(= \frac{1}{2 } (5×6)= \frac{1}{2} (30)=15 \)
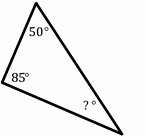
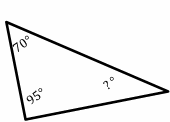
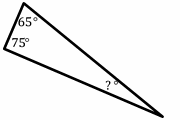
Exercises for Solving Triangles
Find the measure of the unknown angle in each triangle.
Download Triangles Worksheet
- \(\color{blue}{45^{\circ}}\)
- \( \color{blue}{ 15^{\circ}}\)
- \( \color{blue}{ 40^{\circ}}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- The Ultimate GED Math Course [Updated for 2024]
- How to Get a GED Certificate?
- 10 Most Common 6th Grade IAR Math Questions
- Full-Length ALEKS Math Practice Test
- 10 Most Common 5th Grade OST Math Questions
- Best Books for Students Preparing for the SAT Math Test
- How to Find the Volume and Surface Area of Rectangular Prisms? (+FREE Worksheet!)
- How to Prepare for the ISEE Lower Level Math Test?
- 10 Most Common PSAT 10 Math Questions
- The Ultimate AFOQT Math Course (+FREE Worksheets & Tests)
What people say about "How to Solve Triangles Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.