Finding the Area Between Two Triangles

Once you have the area of each triangle, you can subtract the smaller triangle’s area from the larger triangle’s area to find the area between them.

A step-by-step guide to finding the area between two triangles

The formula of the area of a triangle is \(\frac{1}{2}× b×h\), in which b is the length of the base of the triangle, and h is the height of the triangle.
To figure out the area of the shaded region, follow these steps:

Here are the general steps for finding the area between two triangles:

1. Identify the two triangles: Take a look at the diagram and identify the two triangles whose area you want to find. Make sure you have the dimensions of each triangle, such as the base and height.
2. Calculate the area of each triangle: Once you have the dimensions of each triangle, use the formula for finding the area of a triangle, which is: Area = 1/2 x base x height Apply this formula to each triangle to find its area.
3. Identify the larger and smaller triangles: Compare the areas of the two triangles to determine which one is larger and which one is smaller.
4. Subtract the area of the smaller triangle from the area of the larger triangle: Once you have identified the larger and smaller triangles, subtract the area of the smaller triangle from the area of the larger triangle. This will give you the area between the two triangles.

Finding Area Between Two Triangles – Example 1

Solution:

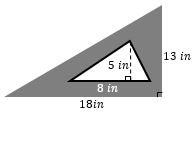
Step 1: Find the area of the larger triangle.
\(18×13=234?, \frac{1}{2}×234=117\)
Step 2: Find the area of the lesser triangle.
\(5×8=40?, \frac{1}{2}×40=20\)
Step 3: Find the area of the shaded region by subtracting the area of the inner shape from the area of the outer shape.
\(117-20=97 in^2\)

Finding Area Between Two Triangles – Example 2

Solution:

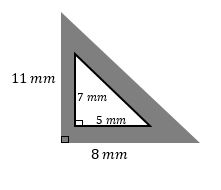
Step 1: Find the area of the larger triangle.
\(11×8=88?, \frac{1}{2}×88=44\)
Step 2: Find the area of the lesser triangle.
\(7×5=35?, \frac{1}{2}×35=17.5\)
Step 3: Find the area of the shaded region by subtracting the area of the inner shape from the area of the outer shape.
\(44-17.5=26.5\)