Triangles
Do you know the features of a triangle? In this article, we are going to complete your information about triangles.
Triangles are closed shapes having three \(3\) angles, three sides, as well as three vertices.
Triangles with \(3\) vertices say \(P, Q,\) and \(R\) are characterized as \(△PQR\). It’s additionally called a \(3\)-sided polygon or a trigon.
Crucial properties of triangles are shown here:
- Triangles have\(3\) sides, angles, and vertices.
- The angle total property of a triangle says the amount of the \(3\) inner triangles is constantly \(180°\). Like with any particular triangle \(PQR\), the angle \(P +\) angle \(Q +\) angle \(R = 180°\).
- Triangle’s inequality property says the amount of the two sides’ length for triangles is bigger than the \(3\)rd side.
- Like in the Pythagorean theorem, with a right triangle, the square of the hypotenuse equates to the quantity of the squares of the additional \(2\) sides such as \((Hypotenuse² = Base² + Altitude²)\).
- The side which is opposite the larger angle is the one that is the longest.
- The outer angle’s property of a triangle says the outer triangle angle always is equivalent to the total of the inside opposite angles.
Triangles can be classified based on angles and sides:
The Absolute Best Book for 4th Grade Students
Related Topics
- Special Right Triangles
- How to Construct Triangles?
- How to Solve Triangles Problems?
- How to Find Missing Sides and Angles of a Right Triangle?
Right Triangles
A right angle’s definition says if one of the triangle’s angles is a right angle – \(90º\), it’s known as a right-angled triangle or merely, a right triangle.
Several critical properties characterize and assist in identifying right triangles.
- The biggest angle is constantly \(90º\).
- The biggest side is known as a hypotenuse, and constantly it’s the side opposite of a right angle.
- The Pythagoras rule governs the dimensions of the sides.
- It can’t contain an obtuse angle.
Acute triangles:
Acute triangles are those classified based on the angles’ measurements. Should every inner angle in the triangle be lower than \(90°\), it’s an acute triangle.
Acute Angle Triangles’ properties are:
- Based on the angle’s sum property, all \(3\) inner angles of the acute triangle combine to form \(180°\).
- Triangles can’t be both right-angled triangles and acute-angled triangles all at once.
- Triangles can’t be acute-angled triangles as well as obtuse-angled triangles all at once.
- The angle’s property of an acute triangle declares the inner angles of acute triangles are constantly fewer than \(90°\) or are in-between (\(0°\) to \(90°\)).
- The side that is opposite to the tiniest angle is the tiniest triangle side.
Obtuse Triangles:
Within geometry, obtuse scalene triangles are defined as triangles with one angle measuring over \(90\) degrees, yet lower than \(180\) degrees, plus the additional \(2\) angles are a smaller amount than \(90\) degrees. All \(3\) sides, as well as the angles, vary in length.
The properties of obtuse scalene triangles are:
- They have \(2\) acute angles as well as \(1\) obtuse angle.
- All its sides and angles are distinct in measurement.
- The total of all \(3\) inner angles equal \(180°\).
A Perfect Book for Grade 4 Math Word Problems!
Triangles – Example 1:
Find the measure of the unknown angle in the triangle
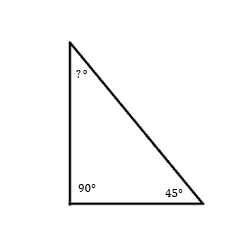
Solution:
The sum of the inner angles of a triangle is \(180°\). So, \(90°\)\(+\)\(45^°\)\(=\)\(135^°\)\(→\)\(180^°\)\(-\) \(135^°\) \(=\) \(45^°\) . The unknown angle is \(45^°\)
Triangles – Example 1:
Find the measure of the unknown angle in the triangle
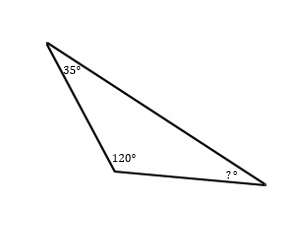
Solution:
The sum of the inner angles of a triangle is \(180°\). So, \(120°\)\(+\)\(35^°\)\(=\)\(155^°\)\(→\)\(180^°\)\(-\) \(155^°\) \(=\) \(25^°\) . The unknown angle is \(25^°\)
Exercises for Triangles
Find the measure of the unknown angle in each triangle.
1)
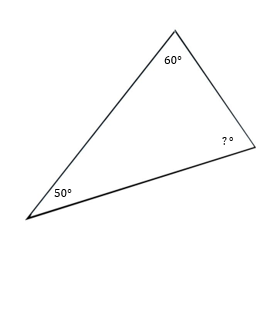
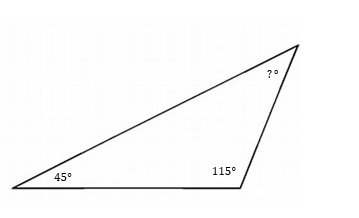
2)
- \(\color{blue}{70^°}\)
- \(\color{blue}{30^°}\)
The Best Math Books for Elementary Students
Related to This Article
More math articles
- How to Find Continuity at a Point?
- 7th Grade Georgia Milestones Assessment System Math FREE Sample Practice Questions
- 3rd Grade NYSE Math FREE Sample Practice Questions
- Even or Odd Numbers
- Top 10 6th Grade PARCC Math Practice Questions
- Managing Math Fear as an Adult
- How to Motivate your Child to Learn Math?
- The Ultimate 7th Grade OAA Math Course (+FREE Worksheets)
- The Ultimate ISEE Lower Level Math Formula Cheat Sheet
- Does ALEKS LockDown Browser Record You?
What people say about "Triangles - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.