How to Apply Trigonometry to General Triangles?
Each triangle is made up of six primary elements ( three sides and three angles). It is sufficient to know the three components of a triangle, one of which must be aside, to completely specify the triangle. Here you learn more about solving triangles.
Each triangle is made up of six primary elements ( three sides and three angles). It is sufficient to know the three components of a triangle, one of which must be aside, to completely specify the triangle. The Law of Sines and the Law of Cosines can be used to get the remaining components in the equation.
Related Topics
The Absolute Best Book to Ace Trigonometry
Step-by-step guide to solving general triangles
There are five basic types of triangles, and we’ll look at them all:
- SSS: If you know the lengths of the \(3\) sides of a triangle, you may follow the Law of Cosines to get one of the angles. It is normally preferable to start with the greatest angle, which is the one that is opposite the longest side. Then, using the Law of Sines, create a percentage to get the second angle. Finally, subtract these angle measurements from \(180°\) to arrive at the third angle measurement.
- To determine the biggest angle in a triangle, the Law of Cosines should be used because if the cosine is positive, the angle is acute; otherwise, it should not be applied. An obtuse angle is one in which the sine of the cosine is less than one. Whenever the cosine is zero, the angle is considered to be a right angle. Once the biggest point of the triangle has been determined, the remaining two angles of the triangle must also be acute.
- The Pythagorean theorem or some other method must be used to determine whether an angle is acute or obtuse if the biggest angle is not discovered using the Law of Cosines but rather the Law of Sines. This is because the sine is positive for both acute and obtuse angles. This necessitates an additional stage in the problem-solving process.
- Use the Law of Cosines if you just need to know the size of one of the angles. It is possible to use the Law of Cosines to identify all the missing angles, but this is more difficult than using the Law of Sines.
- SAS: The Law of Cosines can be used to solve for the third side of a triangle if two sides and the included angle are known. The smallest of the two remaining angles can be found by applying the Law of Sines to the problem. It is the angle on the opposite side of the shortest or shortest side, not the longest. To get the third angle, take these two measurements and subtract \(180°\) from them. The Law of Cosines can be used to discover the two missing angles once more, however, this method is generally more difficult to solve than one based on the Law of Sines.
- ASA: If you know two angles and a triangle’s included side, subtract these angle measurements from \(180°\) to determine the third angle. Next, build up proportions using the Law of Sines to get the lengths of the two missing sides. It is possible to calculate the length of the third side using the Law of Cosines, but why bother when you can just apply the Law of Sines?
- AAS: If you know two angles and a non-included side of a triangle, subtract these angles from \(180°\) to determine the third angle. Next, build up proportions using the Law of Sines to get the length of the two missing sides. In this case, one of the two supplied angles is direct across from the other side. Use the Law of Sines to compute the length of the side opposite the second supplied angle if all that is required.
- SSA: This is referred to as the “ambiguous case.” If you know two sides of a triangle and one non-included angle, there are six alternative configurations; two if the supplied angle is obtuse or right, and four if the given angle is acute.
Solving General Triangles – Example 1:
(SSS) Find the difference between the largest and smallest angles of a triangle.
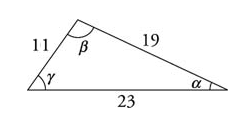
First, use the law of cosines to find the size of the largest angle \((β)\):
\(cos B =\frac {c^2+a^2-b^2}{2ca}\)
\(cos β = \frac {19^2+11^2-23^2}{2(19)(11)}=\frac{361+121-529}{418}=\frac{-47}{418}=-0.112\)
\( β ≅ 96.45^\circ\)
Then, use the law of sines to find the size of the smallest angle \((α)\):
\(\frac {sin A}{a}=\frac {sin B}{b}=\frac {sin C}{c}\)
\(\frac {sin\ α }{11}=\frac {sin\ 96.45}{23}\)
\( sin\ α =\frac{11× sin\ 96.45}{23}=\frac {11 × 0.99}{23}=\frac {10.89}{23}=0.47\)
\( α ≅ 28.37^\circ\)
Now, the difference between the largest and smallest angle is:
\( 96.45^\circ\ – 28.37^\circ=68.08 ^\circ\ \)
Solving General Triangles – Example 2:
(SAS) Find the length of the third side of the triangle.
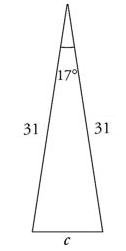
To find side \(c\) use the law of cosines: \(c^2=a^2+b^2-2ab .\cos C\)
\(c^2=31^2+31^2-2(31)(31)(cos 17)=961+961-(1922 × cos 17)=1,922-(1,922 × 0.96)=1,922-1845.12=76.88\)
\(c^2=76.88→ c=\sqrt{76.88}= 8.77\)
Exercises for Solving General Triangles
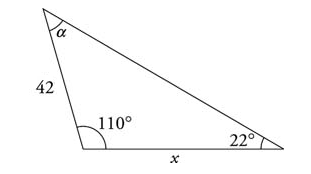
- (AAS) Find the value of \(x\) in the triangle.
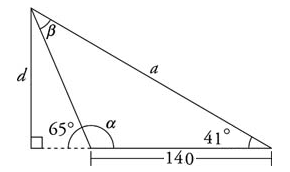
- (ASA) Find the value of \(d\) in the triangle.
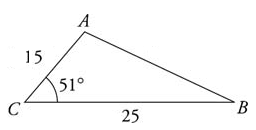
- \(\color{blue}{83.32}\)
- \(\color{blue}{311.95}\)
- \(\color{blue}{19.44}\)
The Best Books to Ace the Trigonometry Test
Related to This Article
More math articles
- 6th Grade PARCC Math Practice Test Questions
- Top Calculators for the PSAT 8/9 Math Test
- HiSET Math Formulas
- Top 10 4th Grade PARCC Math Practice Questions
- How to Inscribe a Regular Polygon within a Circle
- Top 10 Tips You MUST Know to Retake the TSI Math
- Top 10 7th Grade MCAS Math Practice Questions
- CBEST Test Facts and FAQs
- 5th Grade ACT Aspire Math Practice Test Questions
- FREE 7th Grade ACT Aspire Math Practice Test
What people say about "How to Apply Trigonometry to General Triangles? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.