The Significance of the Unit Circle in Trigonometric Functions

Introduction to the Unit Circle

A unit circle is a circle with a radius of \(1\), centered at the origin \((0, 0\)) in the cartesian coordinate system. The main purpose of unit circle in trigonometry is to relate angles to the coordinates of points on the circle, helps defining trigonometric functions like sine, cosine and tangent.

It simplifies trigonometric calculations and is a fundamental tool for solving various mathematical and geometric problems, especially those involving angles and periodic phenomena.

In unit circle, angles increase counter clockwise, and decrease clockwise. So for example: \(-1^\circ = +359^\circ\) The unit circle is divided into \(4\) equal quarters, each called a “quadrant”, starting from top-right quarter which is first quadrant and includes angles from \(0^\circ\) to \(90^\circ\), and so on. Since each quadrant starts where the previous one ends, the \(90^\circ\) angle is actually considered in the \(2^{nd} \) quadrant, \(180^\circ\) in the \(3^{rd}\) and \(270^\circ\) on the \(4^{th}\). This avoids overlap between quadrants.

Significance of Quadrants in Trigonometry

In some trigonometry problems, it is required to know the sign of each trigonometric function (positive or negative), and not necessarily their exact value. Each quadrant has defined signs for trigonometric functions. Here is a list of positive trigonometric functions in each quadrant:

1. All functions are positive
2. Sine and cosecant are positive
3. Tangent and cotangent are positive
4. Cosine and secant are positive.

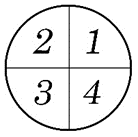
For instance, \(271^\circ\) is in the \(4^{th}\)quadrant and for this angle, only cosine and secant are positive.

Coordinates on the Unit Circle

Any angle, corresponds to a specific point on the circumference of the unit circle. The x-coordiante of that point is the cosine value of that angle, and the y-coordinate is the sine value.

For example, at \(30^\circ\) or \(\frac{\pi}{6}\) radians, the point on the unit circle has the x-coordinate of \(\frac{\sqrt{3}}{2}\), which is cosine of  \(30^\circ\), and a y-coordinate of \(\frac{1}{2}\), which is sine of \(30^\circ\). Similarly, for \(45^\circ\) or \(\frac{\pi}{6}\) radians, sine and cosine are equal \(\frac{\sqrt{2}}{2}\)

Extending to Other Trigonometric Functions

Now that we know how to find the values for sine and cosine of an angle, we can use them to find the values for other trigonometric functions. \(\frac{\sin x}{\cos x} = \tan x\) , and the inverse of tangent, is cotangent.

Secant is the inverse of cosine \((\frac{1}{\cos x})\) and cosecant is the inverse of sine \((\frac{1}{\sin x})\)

For example, for the \(\frac{\pi}{4}\) angle, we have:

\(\tan \left(\frac{\pi}{4}\right) = \frac{\sin \left(\frac{\pi}{4}\right)}{\cos \left(\frac{\pi}{4}\right)} = \frac{\sqrt{2}/2}{\sqrt{2}/2} = 1 = \cot \left(\frac{\pi}{4}\right)\)

\(\sec \left(\frac{\pi}{4}\right) = \frac{1}{\cos \left(\frac{\pi}{4}\right)} = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}\)

Symmetry in Trigonometric Functions

• An even function is symmetric around the y-axis, meaning \(f(x)=f(-x)\), for all \(x\).

• An odd function is symmetric with respect to the origin, satisfying \(f(x)=-f(-x)\), for all \(x\).

For example, \(\sin x\) is odd, while \(\cos x\) is even. This can be helpful when we want to convert trigonometric functions to each other. For example, \(\sin 120^\circ = +0.86\), while \(\sin (-120^\circ) = -0.86\) . and from unit circle, we know that \(-120^\circ = 240^\circ\) , since \(0\) and \(360\) are basically in the same place, so: \(360^\circ – 120^\circ = 240^\circ\)

\(\begin{align*} \sin^2 \left(\frac{\pi}{4}\right) + \cos^2 \left(\frac{\pi}{4}\right) &= \left( \frac{\sqrt{2}}{2} \right)^2 + \left( \frac{\sqrt{2}}{2} \right)^2 \\&= \frac{2}{4} + \frac{2}{4} \\&= \frac{1}{2} + \frac{1}{2} \\&= 1\end{align*}\)

Trigonometric Identities and the Unit Circle

There are various trigonometric identities that help to convert angles of trigonometric functions to other angles, trigonometric functions to one another, eliminate/create exponents, and so on.

These identities can mix up with each other to generate new identities. Some of them are used frequently in trigonometry, while others not as often. For instance, the identity \(\sin^2 x + \cos^2 x = 1\)

Is used very often, and many other useful identities are derived from it. Let’s test it for \(45^\circ\):

Here are a list of useful trigonometric identities:

\(\sin 2\theta = 2 \sin \theta \cos \theta\)

\(\cos 2\theta = 1 – 2\sin^2 \theta = 2\cos^2 \theta – 1 = \cos^2 \theta – \sin^2 \theta = \frac{\cot^2 \theta – 1}{2\cot \theta}\)

\(\tan 2\theta = \frac{2 \tan \theta}{1 – \tan^2 \theta}\)

\(\cos^2 \theta = \frac{1 + \cos 2\theta}{2}\)

\(\sin^2 \theta = \frac{1 – \cos 2\theta}{2}\)

\(\sin(a + b) = \sin a \cdot \cos b + \sin b \cdot \cos a\)

\(\sin(a – b) = \sin a \cdot \cos b – \sin b \cdot \cos a\)

\(\cos(a + b) = \cos a \cdot \cos b – \sin a \cdot \sin b\)

\(\cos(a – b) = \cos a \cdot \cos b + \sin a \cdot \sin b\)

\(\tan(a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b}\)

\(\tan(a – b) = \frac{\tan a – \tan b}{1 + \tan a \cdot \tan b}\)

\(\cot(a + b) = \frac{\cot a \cdot \cot b – 1}{\cot b + \cot a}\)

\(\cot(a – b) = \frac{\cot a \cdot \cot b + 1}{\cot b – \cot a}\)

\(\sin a + \sin b = 2 \sin \left(\frac{a + b}{2}\right) \cdot \cos \left(\frac{a – b}{2}\right)\)

\(\sin a – \sin b = 2 \cos \left(\frac{a + b}{2}\right) \cdot \sin \left(\frac{a – b}{2}\right)\)

\(\cos a + \cos b = 2 \cos \left(\frac{a + b}{2}\right) \cdot \cos \left(\frac{a – b}{2}\right)\)

\(\cos a – \cos b = -2 \sin \left(\frac{a + b}{2}\right) \cdot \sin \left(\frac{a – b}{2}\right)\)

\(\tan x + \tan y = \frac{\sin(x + y)}{\cos x \cdot \cos y}\)

\(\tan x – \tan y = \frac{\sin(x – y)}{\cos x \cdot \cos y}\)

\(\cot x + \cot y = \frac{\sin(x + y)}{\sin x \cdot \sin y}\)

\(\cot x – \cot y = \frac{\sin(y – x)}{\sin x \cdot \sin y}\)

\(\sin a \cdot \cos b = \frac{1}{2}[\sin(a + b) + \sin(a – b)]\)

\(\cos a \cdot \cos b = \frac{1}{2}[\cos(a + b) + \cos(a – b)]\)

\(\sin a \cdot \sin b = -\frac{1}{2}[\cos(a + b) – \cos(a – b)]\)

\(\sin 3a = -4 \sin^3 a + 3 \sin a\)

\(\cos 3a = 4 \cos^3 a – 3 \cos a\)