The Law of Cosines

The law of cosines describes the relationship between the length of the sides of a triangle and the cosine of the angle formed by the triangle. It is often referred to as the cosine rule.

Related Topics

• The Law of Sines
• How to Find Missing Sides and Angles of a Right Triangle
• How to Evaluate Trigonometric Function
• How to Solve Angles and Angle Measure

Step-by-step guide to the law of cosines

If the angles of an oblique triangle are measured by \(A\), \(B\), and \(C\) and \(a\), \(b\), and \(c\) are the lengths of the sides opposite the corresponding angles, then the square of one side of a triangle is equal to the total of the squares of the other two sides minus twice the product of the two sides plus the cosine of the included angle.

\(a^2=b^2+c^2-2bc .\cos A\)

\(b^2=a^2+c^2-2ac .\cos B\)

\(c^2=a^2+b^2-2ab .\cos C\)

Solving for the cosines gives the equivalent formulas:

\(cos A=\frac {b^2+c^2-a^2}{2bc}\)

\(cos B=\frac {c^2+a^2-b^2}{2ca}\)

\(cos C=\frac {a^2+b^2-c^2}{2ab}\)

The Law of Cosines – Example 1:

In the \(ABC\) triangle, find the remaining side.

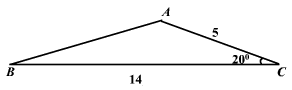
To find side \(c\) use the law of cosines: \(c^2=a^2+b^2-2ab .\cos C\)

\(a=14, b=5, C=20\)

\(c^2\)\(=14^2+5^2-2(14)(5)(cos 20)=(196+25)-(140×cos 20)=221-(140×0.94)=221-131.6=89.4\)

\(c^2=89.4\) → \(c=\sqrt{89.44}= 9.45\)

The Law of Cosines – Example 2:

Find the angle \(B\) in the \(ABC\) triangle.

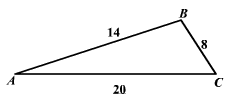
To find angle \(B\) use the law of cosines: \(cos B=\frac {c^2+a^2-b^2}{2ca}\)

\(b=20, a=8, c=14\)

\(cos B= \frac {14^2+8^2-20^2}{2(14)(8)} =\frac {196+ 64 – 400}{176}=\frac{-140}{224}=-0.625\)

Since \(cosB\) is negative, \(B\) is an obtuse angle.

\(B≅128.69 ^\circ \)

Exercises for the Law of Cosines

In the ABC triangle, find the side of c.

1.

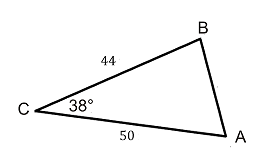
2.

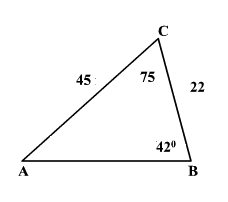
3.

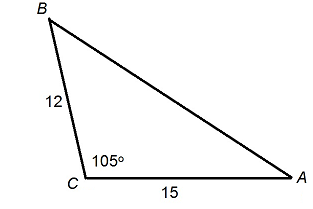
1. \(\color{blue}{31.12}\)
2. \(\color{blue}{44.68}\)
3. \(\color{blue}{21.49}\)