How to Find Missing Sides and Angles of a Right Triangle? (+FREE Worksheet!)
Learn how to find the missing sides or angles of a right triangle when one length and one angle are provided.
Related Topics
- How to Evaluate Trigonometric Function
- How to Solve Angles and Angle Measure
- How to Solve Coterminal Angles and Reference Angles
- How to Solve Trig Ratios of General Angles
Step by step guide to finding missing sides and angles of a Right Triangle
- By using Sine, Cosine or Tangent, we can find an unknown side in a right triangle when we have one length, and one angle (apart from the right angle).
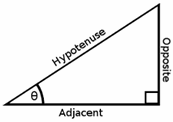
- Adjacent, Opposite and Hypotenuse, in a right triangle is shown below.
- Recall the three main trigonometric functions:
SOH – CAH – TOA, \(sin\) \(θ=\frac{opposite}{hypotenuse}\), \(Cos\) \(θ=\frac{adjacent}{hypotenuse}\), \(tan\) \(θ=\frac{opposite}{adjacent}\)
Missing Sides and Angles of a Right Triangle – Example 1:
Find AC in the following triangle. Round answers to the nearest tenth.
Solution: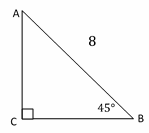 
\(sin\) \(θ=\frac{opposite}{hypotenuse}\). \(sin\) \(45^\circ=\frac{AC}{8}→8 ×sin 45^\circ=AC\),
now use a calculator to find \(sin\) \(45^\circ\). \(sin\) \(45^\circ=\frac{\sqrt{2}}{2}→\cong 0.70710\)
AC\(=\) \( 0.70710 \) \(×\) \( 8 \) \( \cong 5.7 \) → AC\(=5.7\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Missing Sides and Angles of a Right Triangle – Example 2:
Find AC in the following triangle. Round answers to the nearest tenth.
Solution: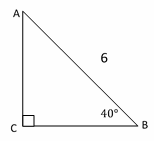 
\(sin\) \(θ=\frac{opposite}{hypotenuse}\). \(sin\) \(40^\circ=\frac{AC}{6}→6 ×\) \(sin\) \(40^\circ=AC\),
now use a calculator to find \(sin\) \(40^\circ\). \(sin\) \(40^\circ\cong 0.642\)
AC\(=\) \( 0.642 \) \(×\) \(6 \) \( \cong 3.9 \) → AC\(= 3.9\)
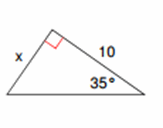
Exercises for Finding Missing Sides and Angles of a Right Triangle
The Best Book to Help You Ace Pre-Algebra
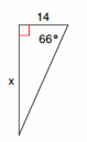
Find the missing side. Round answers to the nearest tenth.
Answers
- \(\color{blue}{31.4}\)
- \(\color{blue}{7.0}\)
- \(\color{blue}{16.2}\)
- \(\color{blue}{31.1}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- Is the PERT Test Hard?
- Can you Teach in California without a Credential?
- How to Use Area Models to Divide Three-digit Numbers By One-digit Numbers
- FREE 8th Grade Georgia Milestones Assessment System Math Practice Test
- Using Decimals and Fractions to Solve One-Step Addition and Subtraction
- How to Distinguishing Numbers: Prime vs. Composite
- Can You Cheat on the ALEKS Test?
- Area Models Unfolded: How to Multiplying Decimals by Two-digit Whole Numbers
- 5th Grade OSTP Math Worksheets: FREE & Printable
- 6th Grade FSA Math FREE Sample Practice Questions
What people say about "How to Find Missing Sides and Angles of a Right Triangle? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.