How to Identify the Function from the Graph
In mathematics, a function is a rule or a relation that maps elements from one set, called the domain, to elements of another set, called the range. The primary characteristic that distinguishes a function from a general relation is that each element in the domain must be associated with exactly one element in the range.

Step-by-step Guide to Identify the Function from the Graph
Here is a step-by-step guide to identify the function from the graph:
Step 1: Foundational Grounding
- Familiarize yourself with the basic definition of a function. Recall that a function assigns to every input exactly one output.
Step 2: Utilize the Vertical Line Test
- The vertical line test is a fundamental tool for identifying functions. Draw or imagine vertical lines across the graph:
- If any vertical line intersects the graph at more than one point, the graph doesn’t represent a function.
- If every vertical line intersects the graph at most once, it is a function.
Step 3: Spot Special Cases
- Some graphs, like those of vertical lines (e.g., \(x=3\)), will fail the vertical line test immediately. These are never functions.
Step 4: Analyze Continuous vs. Discontinuous Graphs
- Continuous graphs have no breaks, jumps, or holes. If such a graph passes the vertical line test, it represents a continuous function.
- Discontinuous graphs may have gaps or jumps. Each separate piece of the graph should be individually subjected to the vertical line test.
Step 5: Evaluate for Implicit Functions
- Some functions, especially those involving circles or ellipses, might not be explicitly solved for one variable. Even if they appear complex, the vertical line test remains a valid tool.
Step 6: Understand Graph Behavior at Asymptotes
- Vertical asymptotes can be tricky. A graph might approach but never cross a vertical asymptote, which can still be consistent with a function. However, if it crosses an asymptote more than once, it fails the function test.
Step 7: Investigate End Behavior and Horizontal Asymptotes
- While the horizontal asymptotes and end behavior don’t directly determine if a graph is a function, they can give insights into the function’s type and characteristics.
Step 8: Distinguish One-to-One Functions with the Horizontal Line Test
- While the vertical line test determines if a graph is a function, the horizontal line test determines if it’s a one-to-one function. If no horizontal line intersects the graph more than once, the function is one-to-one.
Step 9: Employ Graphing Tools and Software
- Utilize tools like Desmos, GeoGebra, or graphing calculators to visualize and manipulate graphs. These can help in understanding complex graphs and verifying if they represent functions.
Step 10: Engage in Comparative Analysis
- Compare the given graph with standard function shapes you know (e.g., linear, quadratic, sine, exponential). Recognizing similarities or patterns can aid in identification.
Step 11: Iterative Verification
- Continuously re-evaluate as you analyze. Sometimes, initial perspectives might not capture all the nuances of a complex graph.
Step 12: Seek Peer Reviews
- Sometimes, discussing with peers or presenting your analysis to others can help spot oversights or provide alternative viewpoints.
By systematically following this multifaceted approach, one can accurately identify whether a given graph, even one with high variation and complexity, represents a function. This process not only focuses on identification but also deepens one’s understanding of the nature and behavior of functions in general.
Examples:
Given the following graph, determine whether the graph is a function or not.
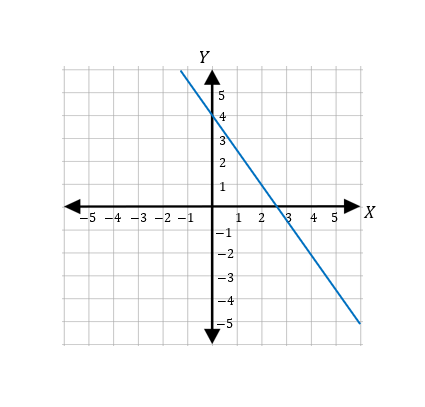
Solution:
Draw a vertical line across the graph such as the line drawn in the graph below. It intersects the graph at most once, So, it is a function.
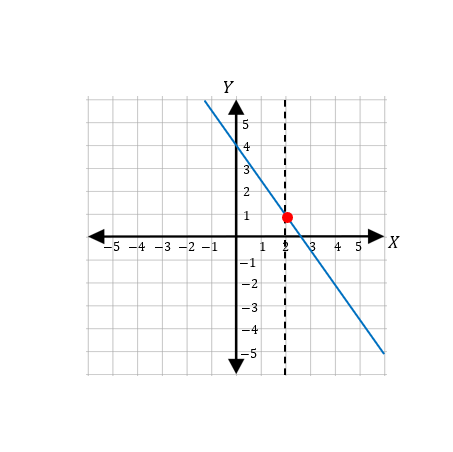
Related to This Article
More math articles
- How to Multiply and Divide Integers? (+FREE Worksheet!)
- How to Graph Quadratic Inequalities? (+FREE Worksheet!)
- The Ultimate Regents Algebra 1 Course (+FREE Worksheets)
- Do My Essay for Me: What Are the Benefits of Remote Learning?
- How to Master the Squeeze Theorem for Calculating Limits
- How to Balance the Scales: Inequalities in Decimal Addition and Subtraction
- Full-Length 6th Grade IAR Math Practice Test-Answers and Explanations
- Top 10 ACT Math Prep Books (Our 2023 Favorite Picks)
- Rounding Rally: Simplifying Decimals to the Nearest Whole
- How to Prepare for the OAR Math Test?


























What people say about "How to Identify the Function from the Graph - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.