How to Graph Quadratic Inequalities? (+FREE Worksheet!)
Want to know how to graph Quadratic inequalities? You can do it in a few simple and easy steps.
Related Topics
- How to Graph Quadratic Functions
- How to Solve a Quadratic Equation
- How to Solve Quadratic Inequalities
Step by step guide to Graphing Quadratic inequalities
- A quadratic inequality is in the form \(y>ax^2+bx+c\) (or substitute \(<,≤,\) or \(≥ \) for \(>\)).
- To graph a quadratic inequality, start by graphing the quadratic parabola. Then fill in the region either inside or outside of it, depending on the inequality.
- Choose a testing point and check the solution section.
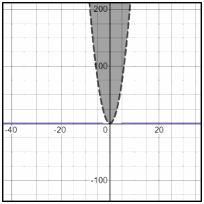
Graphing Quadratic inequalities – Example 1:
Sketch the graph of \(y>3x^2\).
Answer:
First, graph \(y=3x^2\)
Since the inequality sing is \(>\), we need to use dash lines.
Now, choose a testing point inside the parabola. Let’s choose \((0,2)\).
\(y>3x^2→2>3(0)^2→2>0\)
This is true. So, inside the parabola is the solution section.
The Absolute Best Books to Ace Pre-Algebra to Algebra II
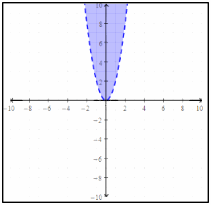
Graphing Quadratic inequalities – Example 2:
Sketch the graph of \(y>2x^2\).
Answer:
First, graph \(y=2x^2\)
Since the inequality sign is \(>\), we need to use dash lines.
Now, choose a testing point inside the parabola. Let’s choose \((0,2)\). \(y>2x^2→2>2(0)^2→2>0\)
This is true. So, inside the parabola is the solution section.
The Best Book to Help You Ace Pre-Algebra
Exercises for Graphing Quadratic inequalities
Sketch the graph of each function.
- \(\color{blue}{y<-2x^2}\)
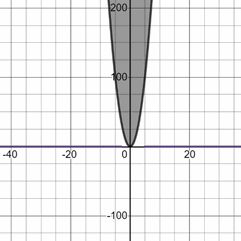
- \(\color{blue}{y≥4x^2}\)
- \(\color{blue}{y<-2x^2}\)
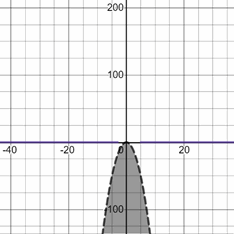
- \(\color{blue}{y≥4x^2}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- How to Study Math Like a Pro
- Word Problems Involving Area of Quadrilaterals and Triangles
- 8th Grade OST Math Worksheets: FREE & Printable
- Area of a Triangle
- How to Find Powers and Roots of Complex Numbers
- Unlocking the Secrets of Inscribed Polygons
- What Skills Do I Need for the ACT Math Test?
- Top 10 Tips to Create an ASTB Math Study Plan
- Decimal Detective: How to Find Numbers with a Specific Sum or Difference
- 5 Best Laptops For Teachers
What people say about "How to Graph Quadratic Inequalities? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.