ACT Math Practice Test Questions

Preparing for the ACT Math test? Try following FREE ACT Math Practice Questions. Reviewing practice questions is the best way to brush up on your Math skills. Here, we walk you through solving 10 common ACT Math practice problems covering the most important math concepts on the ACT Math test.

These ACT Math practice questions are designed to be similar to those found on the real ACT Math test. They will assess your level of preparation and will give you a better idea of what to study for your exam.

The Absolute Best Book to Ace the ACT Math Test

10 Sample ACT Math Practice Questions

1- If \(40 \%\) of a class are girls, and \(25 \%\) of girls play tennis, what percent of the class play tennis?

A. \(10 \%\)

B. \(15 \%\)

C. \(20 \%\)

D. \(40 \%\)

E. \(80 \%\)

2- \(5^{\frac{7}{3}}× 5^{\frac{2}{3}} = \)?

A. \(5^1\)

B. \(5^2\)

C. \(5^3\)

D. \(5^4\)

E. \(5^5\)

3- Simplify.
\(2x^2+3y^5-x^2+2z^3-2y^2+2x^3-2y^5+5z^3\)

A. \(3x^2-2y^2+y^5+7z^3\)

B. \(x^2+2x^3-2y^2+y^5+7z^3\)

C. \( x^2+2x^3+3y^5+7z^3\)

D. \(x^2+2x^3-2y^2+5y^5+7z^3\)

E. \( x^2+2x^3-2y^2+7z^3\)

4- In five successive hours, a car travels 40 km, 45 km, 50 km, 35 km, and 55 km. In the next five hours, it travels with an average speed of 50 km per hour. Find the total distance the car traveled in 10 hours.

A. 425 km

B. 450 km

C. 475 km

D. 500 km

E. 1000 km

5- From last year, the price of gasoline has increased from $1.25 per gallon to $1.75 per gallon. The new price is what percent of the original price?

A. \(72 \%\)

B. \(120 \%\)

C. \(140 \%\)

D. \(160 \%\)

E. \(180 \%\)

6- If \(x\) is a real number, and if \(x^3+18=130\), then \(x\) lies between which two consecutive integers?

A. 1 and 2

B. 2 and 3

C. 3 and 4

D. 4 and 5

E. 5 and 6

7- if \(\frac{3x}{16} = \frac{x – 1}{4}\) =?

A. \(\frac{1}{4}\)

B. \(\frac{3}{4}\)

C. 3

D. 4

E. \(\frac{9}{4}\)

8- If \((x-2)^3=27\) which of the following could be the value of \((x-4)(x-3)\)?

A. 1

B. 2

C. 6

D. \(-1\)

E. \(-2\)

9- Simplify \((–5 + 9i)(3 + 5i)\)?

A. \(6 – 2i\)

B. \(60 – 2i\)

C. \(6 +2i\)

D. \(-60 +2i\)

E. \(2i\)

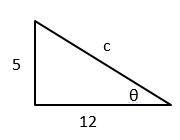
10- If tan \(\theta = 5/12\) and sin \(\theta > 0\), then cos \(\theta\) =?

A. \(-\frac{5}{13}\)

B. \(\frac{12}{13}\)

C. \(\frac{13}{12}\)

D. \(-\frac{12}{13}\)

E. 0

Best ACT Math Prep Resource for 2022

Answers:

2- C
\(5^{\frac{7}{3}}× 5^{\frac{2}{3}} = 5 ^{\frac{7}{3} + \frac{2}{3}}= 5^{\frac{9}{3}}= 5^3\)

3- B
\(2x^2+3y^5-x^2+2z^3-2y^2+2x^3-2y^5+5z^3=2x^2-x^2+2x^3-2y^2+3y^5-2y^5+2z^3+5z^3=x^2+2x^3-2y^2+y^5+7z^3\)

4- C
Add the first 5 numbers. \(40 + 45 + 50 + 35 + 55 = 225\)
To find the distance traveled in the next 5 hours, multiply the average by number of hours.
\(Distance = Average × Rate = 50 × 5 = 250\)
Add both numbers. \(250 + 225 = 475\)

5- C
The question is this: 1.75 is what percent of 1.25?
Use percent formula:
\(part = \frac{percent}{100}× whole \)
\(1.75 = \frac{percent}{100}× 1.25 ⇒ 1.75 = \frac{percent ×1.25}{100}⇒175 = percent ×1.25 ⇒ percent =\frac{175}{1.25}= 140\)

6- D
Solve for \(x\).
\(x^3+18=130\)
\(x^3=112\)
Let’s review the options.
A. 1 and \(2. 1^3 = 1\) and \(2^3 = 8\), 112 is not between these two numbers.
B. 2 and 3. \(2^3 = 8 \space and \space 3^3 = 27\), 112 is not between these two numbers.
C. 3 and 4. \(3^3 = 27\) and \(4^3 = 64\), 112 is not between these two numbers.
D. 4 and 5. \(4^3 = 64 \) and \(5^3 = 125\), 112 is between these two numbers.
E. 5 and 6. \(5^3 = 125\) and \(6^3 = 216\), 112 is not between these two numbers.

7- D
Solve for \(x\).\(\frac{3x}{16} = \frac{x – 1}{4}\)
Multiply the second fraction by 4.
\(\frac{3x}{16}=\frac{4(x-1)}{4×4}\)
\(3x=4x-4\)
\(0=x-4\)
\(4=x\)

8- B
\((x-2)^3=27→x-2=3→x=5
→(x-4)(x-3)=(5-4)(5-3)=(1)(2)=2\)

9- D
We know that: \(i=√(-1)⇒i^2=-1\)
\( (-5+9i)(3+5i)=-15-25i+27i+45i^2=-15+2i-45=2i-60\)

10- B
\(tanθ=\frac{opposite}{adjacent}\)
\(tanθ=\frac{5}{12}\)⇒ we have the following right triangle. Then
\(c=√(5^2+12^2 )=√(25+144)=√169=13\)
\(\frac{adjacent}{hypotenuse}=\frac{12}{13}\)

College Entrance Tests

Looking for the best resource to help you succeed on the ACT Math test?

The Best Books to Ace the ACT Math Test