10 Most Common ParaPro Math Questions
Are you preparing for the ParaPro Math test? Looking for the most common mathematics questions on the ParaPro Math test to help you get familiar with the test content? If so, then you are in the right place. For additional educational resources, visit the U.S. Department of Education website.
The Math section of ParaPro can be a challenging area for many test-takers, but with enough patience, it can be manageable and even enjoyable!
Preparing for the ParaPro Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the actual ParaPro test can help you reduce those pre-test jitters. Here’s your chance to work on the 10 most common ParaPro Math questions to help you know what to expect and what to practice most. Try these 10 most common ParaPro Math questions to hone your Math skills and to see if your math skills are up to date on what’s being asked on the exam, or if you still need more practice.
Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the ParaPro Math Test
\%, \frac{2}{3} , \frac{4}{5} \)
D. \(\frac{2}{3} , 67\%, 0.68, \frac{4}{5} \)
6- The mean of \(50\) test scores was calculated as \(88\). But, it turned out that one of the scores was misread as \(94\), but it was \(69\). What is the mean?
A. \(85\)
B. \(87\)
C. \(87.5\)
D. \(88.5\)
7- Two dice are thrown simultaneously. What is the probability of getting a sum of \(6\) or \(9\)?
A. \(\frac{1}{3} \)
B. \(\frac{1}{4} \)
C. \(\frac{1}{6} \)
D. \(\frac{1}{2} \)
8- Jason is \(9\) miles ahead of Joe running at \(5.5\) miles per hour, and Joe is running at the speed of \(7\) miles per hour. How long does it take Joe to catch Jason?
A. \(3\) hours
B. \(4\) hours
C. \(6\) hours
D. \(8\) hours
9- \(55\) students took an exam and \(11\) of them failed. What percent of the students passed the exam?
A. \(40\%\)
B. \(60\%\)
C. \(80\%\)
D. \(20\%\)
10- What is the volume of a box with the following dimensions?
Height \(= 4\) \(cm\), Width \(= 5 cm\) , Length \(= 6 cm\)
A. \(15 cm^3\)
B. \(60 cm^3\)
C. \(90 cm^3\)
D. \(120 cm^3\)
Best ParaPro Math Prep Resource for 2026
Answers:
1- D
Simplify.
\(6x^2 y^3 (2x^2 y)^3= 6x^2 y^3 (8x^6 y^3 ) = 48x^8 y^6\)
2- 28 For education statistics and research, visit the National Center for Education Statistics.
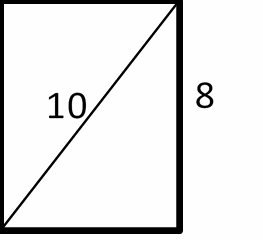
Let x be the width of the rectangle. Use Pythagorean Theorem:
\(a^2 + b^2 = c^2\)
\(x^2 + 8^2 = 10^2 {\Rightarrow} x^2 + 64 = 100 {\Rightarrow} x^2 = 100 – 64 = 36 ⇒ x = 6\)
Perimeter of the rectangle \(= 2 (length + width) = 2 (8 + 6) = 2 (14) = 28\) For education statistics and research, visit the National Center for Education Statistics.
3- D
Isolate and solve for \(x\).
\(\frac{2}{3} x+\frac{1}{6} = \frac{1}{3} {\Rightarrow} \frac{2}{3} x= \frac{1}{3} -\frac{1}{6} = \frac{1}{6} {\Rightarrow} \frac{2}{3} x= \frac{1}{6} \)
Multiply both sides by the reciprocal of the coefficient of \(x\).
\((\frac{3}{2}) \frac{2}{3} x= \frac{1}{6} (\frac{3}{2}) {\Rightarrow} x= \frac{3}{12}=\frac{1}{4}\)
4- D
The probability of choosing a Hearts is \(\frac{13}{52}=\frac{1}{4} \)
5- D
Change the numbers to decimals and then compare.
\(\frac{2}{3} = 0.666… \)
\(0.68 \)
\(67\% = 0.67\)
\(\frac{4}{5} = 0.80\)
Therefore
\(\frac{2}{3} < 67\% < 0.68 < \frac{4}{5}\)
6- C
average (mean)\( =\frac{(sum \space of \space terms)}{(number \space of \space terms)} {\Rightarrow} 88 = \frac{(sum \space of \space terms)}{50} {\Rightarrow} sum = 88 {\times} 50 = 4400\)
The difference of \(94\) and \(69\) is \(25\). Therefore, \(25\) should be subtracted from the sum.
\(4400 – 25 = 4375\)
\(mean = \frac{(sum of terms)}{(number of terms)} ⇒ mean = \frac{(4375)}{50}= 87.5\)
7- B
To get a sum of \(6\) for two dice, we can get \(5\) different options:
\((5, 1), (4, 2), (3, 3), (2, 4), (1, 5)\)
To get a sum of \(9\) for two dice, we can get \(4\) different options:
\((6, 3), (5, 4), (4, 5), (3, 6)\)
Therefore, there are \(9\) options to get the sum of \(6\) or \(9\).
Since we have \(6 × 6 = 36\) total options, the probability of getting a sum of \(6\) and \(9\) is \(9\) out of \(36\) or \(\frac{1}{4}\).
8- C
The distance between Jason and Joe is \(9\) miles. Jason is running at \(5.5\) miles per hour, and Joe is running at the speed of \(7\) miles per hour. Therefore, every hour, the distance is \(1.5\) miles less. \(9 \div 1.5 = 6\)
9- C
The failing rate is \(11\) out of \(55 = \frac{11}{55} \)
Change the fraction to a percent:
\( \frac{11}{55} {\times} 100\%=20\% \)
\(20\) percent of students failed. Therefore, \(80\) percent of students passed the exam.
10- D
Volume of a box \(= length \times width \times height = 4 \times 5 \times 6 = 120\)
The Best Book to Ace the ParaPro Test
More from Effortless Math for ParaPro Test …
Don’t know the top websites for learning ParaPro math?
We help you gain this knowledge: Top 10 Free Websites for ParaPro Math Preparation
Need help preparing for the ParaPro math test?
We will help you with this: How to Prepare for the ParaPro Math Test?
Looking for resources to practice more ParaPro math test?
Try ParaPro Math Practice Test Questions!
The Perfect Prep Books for the ParaPro Math Test
Have any questions about the ParaPro Test?
Write your questions about the ParaPro or any other topics below and we’ll reply!
Related to This Article
More math articles
- 10 Most Common 4th Grade PSSA Math Questions
- How to Interpret Histogram? (+FREE Worksheet!)
- How to Find Mean Absolute Deviation?
- How to Understand Vocabulary of Financial Institutions
- How to Prepare for Math Exams: Study Tips & Tricks
- 3rd Grade CMAS Math Worksheets: FREE & Printable
- Derivatives Demystified: Everything You Need to Know
- The Ultimate SBAC Algebra 1 Course (+FREE Worksheets)
- Best Laptop for High School Students in 2026
- How to Solve the Ambiguous Case (SSA) in Trigonometry
What people say about "10 Most Common ParaPro Math Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.