How to Graph Quadratic Functions? (+FREE Worksheet!)
Learn how to Graph Quadratic Functions in the vertex or standard forms following a few simple steps.
Related Topics
- How to Solve Quadratic Inequalities
- How to Solve a Quadratic Equation
- How to Graph Quadratic Inequalities
Step by step guide to Graphing Quadratic Functions
- Quadratic functions in vertex form: \(y=a(x – h)^2+k\) where \((h,k)\) is the vertex of the function. The axis of symmetry is \(x=h\)
- Quadratic functions in standard form: \(y=ax^2+bx+c\) where \(x=-\frac{b}{2a}\) is the value of \(x\) in the vertex of the function.
- To graph a quadratic function, first find the vertex, then substitute some values for \(x\) and solve for \(y\).
A Perfect Practice Workbook for Algebra I
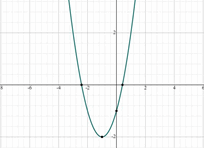
Graphing Quadratic Functions – Example 1:
Sketch the graph of \(y=(x+1)^2-2\).
Solution:
First, recall that a Quadratic function in vertex form is \(y=a(x – h)^2+k\) where \((h,k)\) is the vertex of the function.
The vertex of \(y=(x+1)^2-2\) is \((-1,-2)\). Substitute zero for \(x\) and solve for \(y\). \(y=(0+1)^2-2=-1\). The \(y\) Intercept is \((0,-1)\).
Now, you can simply graph the quadratic function.
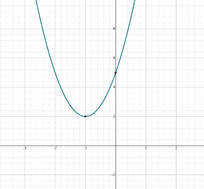
Graphing Quadratic Functions – Example 2:
Sketch the graph of \(y=3(x+1)^2+2\).
Solution:
First, recall that a Quadratic function in vertex form is \(y=a(x – h)^2+k\) where \((h,k)\) is the vertex of the function.
The vertex of \(y=3(x+1)^2+2\) is \((-1,2)\). Substitute zero for \(x\) and solve for \(y\). \(y=3(0+1)^2+2=5\). The \(y\) Intercept is \((0,5)\).
Now, you can simply graph the quadratic function.
Exercises for Graphing Quadratic Functions
Best Algebra Prep Resource
Sketch the graph of each function. Identify the vertex and axis of symmetry.
- \(\color{blue}{y = 3(x-5)^2-2}\)
- \(\color{blue}{y=x^2-3x+15}\)
Download Graphing Quadratic Functions Worksheet
- \(\color{blue}{y = 3(x-5)^2-2}\)
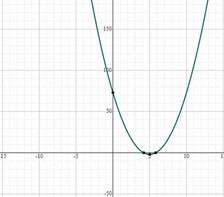
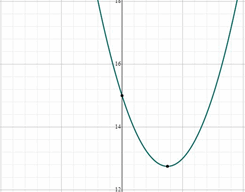
- \(\color{blue}{y=x^2-3x+15}\)
The Absolute Best Books to Ace Algebra
Related to This Article
More math articles
- Top Calculator for the PSAT 10 Math Test: Quick Review
- Math Café: How to Learn the Art of Writing and Solving Two-variable Equations
- 10 Most Common 3rd Grade STAAR Math Questions
- FREE ASTB Math Practice Test
- How to Find the Equation of a Regression Line and Interpret Regression Lines
- How to Graph Triangles and Quadrilaterals?
- FREE FTCE Math Practice Test
- How to Motivate your Child to Learn Math?
- 5th Grade NDSA Math Worksheets: FREE & Printable
- Empower Your Homeschooling Efforts with ‘Pre-Algebra for Beginners’
What people say about "How to Graph Quadratic Functions? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.