Full-Length 6th Grade IAR Math Practice Test-Answers and Explanations

Did you take the 6th Grade IAR Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
6th Grade IAR Math Practice Test Answers and Explanations
1- Choice B is correct
Plug in the value of \(x\) and \(y\) and use order of operations rule. \(x=2\) and \(y=-3\)
\(5(4x-3y)-7y^2=5(4(2)-3(-3))-7(-3)^2=5(8+9)-7(9)=5(17)-63=85-63=22\)
2- Choice C is correct
For one hour he earns \($18\), then for \(t\) hours, he earns \($18t\). If he wants to earn at least \($78\), therefore, the number of working hours multiplied by \(18\) must be equal to \(78\) or more than \(78\). \(18t≥78\)
3- Choice B is correct
\((108-(3×9))÷9=9^3÷81=9\)
4- Choice B is correct
The ratio of boys to girls is \(3∶5\). Therefore, there are \(3\) boys out of \(8\) students. To find the answer, first, divide the total number of students by \(8\), then multiply the result by\(3\).
\(240÷8=30 ⇒ 30×3=90\)
5- Choice A is correct
Probability \(=\frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes} = \frac{9}{9+15+14+16}=\frac{9}{54}=\frac{1}{6}=0.16\)
6- Choice D is correct
Let’s compare each fraction: \(\frac{2}{3}<\frac{3}{4}<\frac{7}{9}<\frac{4}{5}\)
Only choice D provides the right order.
7- Choice B is correct
Let \(y\) be the width of the rectangle. Then; \(14×y=84→y=\frac{84}{14}=6\)
8- Choice B is correct
\(4×\frac{5}{16}=\frac{20}{16}=1.25\)
A. \(1.25>2\)
B. \(1<1.25<2\) This is the answer!
C. \(\frac{3}{8}=1.25\)
D. \(1.25=2^2\)
9- Choice B is correct
In any rectangle, The measure of the sum of all the angles equals \(180^\circ\).
10- Choice C is correct
\(\frac{824}{17}=48.5\)
11- The answer is \(7^2\).
\(588=2^2×3^1×7^2\)
12- Choice B is correct
The area of the trapezoid is: ????\(=\frac{(???? \space 1+???? \space 2)}{2}
×ℎ???ℎ?=\frac{12+10}{2}?=?→11?=?→?=\frac{A}{11}\)
13- Choice B is correct
\(\frac{72}{8}=9, \frac{648}{72}=9, \frac{5832}{648}=9\), Therefore, the factor is \(9\).
14- Choice C is correct
Simplify each option provided.
A. \(13-(3×6)+(7×(-6))=13-18+(-42)=-5-42=-47\)
B. \((\frac{25}{400})+(\frac{7}{50})=\frac{25}{400}+\frac{56}{400}=\frac{81}{400}\)
C. \(((22×\frac{30}{6})-(7×\frac{144}{12}))×\frac{18}{2}=(110-84)×9=26×9=234\) (this is the answer)
D. \((\frac{6}{24}+\frac{12}{33})-50=(\frac{1}{4}+\frac{1}{3})-50=(\frac{3}{12}+\frac{4}{12})-50=\frac{7}{12}-50=\frac{-593}{15}\)
15- Choice D is correct
To find the discount, multiply the number \((100\%- rate \space of \space discount)\)
Therefore; \(450(100\%-16\%)=450(1-0.16)=450-(450×0.16)\)
The Absolute Best Book to Ace the IAR Math Test
16- Choice A is correct
\(1,400\) out of \(11,900\) equals to \(\frac{1,400}{11,900}=\frac{200}{1,700}=\frac{2}{17}\)
17- Choice C is correct
The opposite of Nicolas’s integer is \(25\). So, the integer is \(-25\). The absolute value of \(25\) is also \(25\).
18- Choice B is correct
Volume of a box = length\( ×\) width \(×\) height \(= 7 × 4 × 12 = 336\)
19- Choice C is correct
\(1\) yard \(= 3\) feet, Therefore: \(33,759 \space ft×\frac{1 \space yd}{3 \space ft}=11,253 \space yd\)
20- Choice B is correct
\(16\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(16\%\) of \(x=38\) \(ml\) ⇒ \(0.16x=38 ⇒ x=38÷0.16=237.5\)
21- Choice C is correct
\((-2)(9x-8)=(-2)(9x)+(-2)(-8)=-18x+16\)
22- Choice D is correct
\(1 pt = 16\) fluid ounces. \(576 ÷ 16 = 36 \)
Then: \(576\) fluid ounces \(= 36 pt\)
23- Choice D is correct
\(1 kg = 1,000 g\) and \(1 g = 1,000 mg\),
\(120 kg = 120 × 1,000 g = 120 × 1,000 × 1,000 = 120,000,000 mg\)
24- Choice C is correct
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{14}{2}=7\).
Area of a circle \(= πr^2=π(7)^2=49π=49×3.14=153.86≅153.9\)
25- Choice B is correct
Average (mean)\(=\frac{sum \space of \space terms}{number \space of \space terms}=\frac{15+17+12+16+21+23}{6}=\frac{104}{6}=17.33\)
26- Choice C is correct
Prime factorizing of \(18=2×3×3\), Prime factorizing of \(24=2×2×2×3\)
\(LCM\) \(= 2×2×2×3×3=72\)
27- Choice B is correct
The coordinate plane has two axes. The vertical line is called the \(y\)-axis and the horizontal is called the \(x\)-axis. The points on the coordinate plane are addressed using the form \((x,y)\). Point \(A\) is one unit on the left side of the \(x\)-axis, therefore its \(x\) value is \(4\) and it is two units up, therefore its \(y\)-axis is \(2\). The coordinate of the point is: \((4, 2)\)
28- Choice B is correct
\(α\) and \(β\) are supplementary angles. The sum of supplementary angles is \(180\) degrees.
\(α+β=180^\circ→α=180^\circ -β=180^\circ-125^\circ=55^\circ\), Then, \(\frac{α}{β}=\frac{55}{125}=\frac{11}{25}\)
29- Choice C is correct
The opposite number of any number \(x\) is a number that if added to \(x\), the result is \(0\). Then:
\(7+(-7)=0\) and \(4+(-4)=0\)
Best 6th Grade IAR Math Prep Resource
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
30- Choice C is correct
\(16=-129+x\), First, subtract \(129\) from both sides of the equation. Then:
\(16+129=-129+x+129 →145=x\)
31- Choice D is correct
\(-5<2x+7≤3\)→ (add (\(-7\)) all sides) \((-7)+(-5)<2x+7+(-7)≤3+(-7) →-12<2x≤-4→\) (divide all sides by \(2\)), \(-6<x≤-2\)
In inequality \(-6<x≤-2\), \(x\) is fewer or equal to \(-2\) and more than \(-6\). Only choice D represents the same inequality on the number line.
32- Choice B is correct
A. Number of books sold in April is: \(690\)
The number of books sold in July is: \(1150→ \frac{690}{1150}≠2\)
B. Number of books sold in July is: \(1150\)
Half the number of books sold in May is: \(\frac{1150}{2} =575→690>575\) (it’s correct)
C. Number of books sold in June is: \(375\)
Half the number of books sold in April is: \(\frac{690}{3}=230→240<375\)
D. \(690+375=1,065>1150\)
33- Choice B is correct
\(51∶18=17∶6, 17×3=51\) and \(8×3=18\)
34- Choice A is correct
There are \(6\) integers from \(9\) to \(15\). Set of numbers that are not composite between \(9\) and \(15\) is: \([{11,13}]\), \(2\) integers are not composite. Probability of not selecting a composite number is: Probability\(= \frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}= \frac{2}{6}=\frac{1}{3}\)
35- Choice A is correct
Number of biology book:\(20\), Total number of books; \(20+59+36=115\)
The ratio of the number of biology books to the total number of books is: \(\frac{20}{115}=\frac{4}{23}\)
36- Choice B is correct
A. \(\frac{5}{8}<0.8→ \frac{5}{8}=0.6\). Therefore, this inequality is not correct.
B. \(23\%<\frac{2}{3} →23\%= 0.23, \frac{2}{3}=0.66\),Therefore \(0.23<0.66\) .
C. \(8<\frac{18}{3} →\frac{18}{3}=6\). Therefore, this inequality is not correct.
D. \(0.6>\frac{7}{9}→ \frac{7}{9}=0.77→0.77>0.6\), this inequality is not correct.
37- Choice A is correct
\(38÷2=19\)
38- The answer is 0.38
\(38\) percent \(= 0.38\)
39- Choice B is correct
Let’s write the inequality for each statement.
A. \(\frac{x}{19}<9\)
B. \(\frac{9}{x}≤19\) This is the inequality provided in the question.
C. \(\frac{x}{9}≤19\)
D. \(\frac{x}{9}<19\)
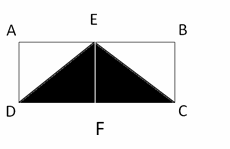
40- Choice C is correct
Since \(E\) is the midpoint of \(AB\), then the area of all triangles \(DAE, DEF, CFE\), and \(CBE\) are equal. The total area of \(ABCD\) is \(180\). So, the area of each triangle is \(180 ÷ 4 = 45\)
The area of the triangle \(ADE\) is: \(45\)
The Most Comprehensive Review for 6th-Grade Students
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- The Importance Of Mathematics For Students Pursuing STEM
- Geometry Puzzle – Critical Thinking 20
- Top 10 4th Grade SBAC Math Practice Questions
- What Skills Do I Need for the ACT Math Test?
- The Ultimate Adults Math Refresher Course (+FREE Worksheets & Tests)
- Tips You MUST Know to Retake the Praxis Core Math Test
- Three and A Half Principles of Extraordinary Techniques for Math Teaching
- Top 10 Free Websites for ACCUPLACER Math Preparation
- The Ultimate AP Calculus BC Course
- How to Define Degrees and Radians
















What people say about "Full-Length 6th Grade IAR Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.