The Law of Sines

When you already know the measurements of 2 factors in a triangular as well as one of the sides, like in the case of ASA or AAS, you may apply the law of sines to determine the measures of the other two angles and the other side.

This law is based on the ratio of the side of the triangle and the angles that are opposite to each other. The greater the width of a side, the greater the width of its opposite angle. The largest side is always on the other side of the most acute angle.

Related Topics

• How to Find Missing Sides and Angles of a Right Triangle
• How to Evaluate Trigonometric Function
• How to Solve Angles and Angle Measure

A step-by-step guide to the law of sines

• The law of sines is:

In a right oblique triangle, if the measurements of the angles are \(A\), \(B\), and \(C\), and the measurements of the length of the sides opposite the corresponding angles are \(a\), \(b\), and \(c\), then the length of each side to the sine of the opposing angle must all be equal.

\(\frac {sin A}{a}=\frac {sin B}{b}=\frac {sin C}{c}\)

\(\frac {a}{sin A}=\frac {b}{sin\ B}=\frac {c}{sin\ C}\)

The Law of Sines – Example 1:

In the ABC triangle, find the sides and the angle.

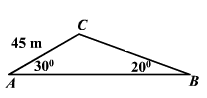
All angles in a triangle sum up to \(180\) degrees. Then:

\(30+20+x=180→ 50+x=180→x=180-50=130 ^\circ \)

To find sides use the law of sines: \(\frac {a}{sin\ A}=\frac {b}{sin\ B}=\frac {c}{sin\ C}\)

\(\frac {a}{sin 30}=\frac {45}{sin\ 20}= \frac {c}{sin 130}\)

Now, use proportional ratios: \(\frac {a}{b}=\frac{c}{d} → a×d=c×b\)

\(\frac {a}{sin 30}=\frac {45}{sin\ 20}\) → \(a=\frac {45 × sin\ 30}{sin 20}=\frac {45 × 0.5}{0.34}=\frac {22.5}{0.34}≅66.18 m\)

\(\frac {45}{sin\ 20}= \frac {c}{sin 130}\) → \(c=\frac {45 × sin 130}{sin 20}=\frac {45 × 0.77}{0.34}=\frac {34.65}{0.34}≅101.91 m\)

The Law of Sines – Example 2:

Find the sides and the angle in the ABC triangle.

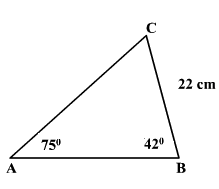
All angles in a triangle sum up to \(180\) degrees. Then:

\(75+42+x=180→ 117+x=180→x=180-117=63 ^\circ \)

To find sides use the law of sines: \(\frac {a}{sin\ A}=\frac {b}{sin\ B}=\frac {c}{sin\ C}\)

\(\frac {22}{sin\ 75}=\frac {b}{sin\ 42}= \frac {c}{sin\ 63}\)

Now, use proportional ratios: \(\frac {a}{b}=\frac{c}{d} → a×d=c×b\)

\(\frac {22}{sin\ 75}=\frac {b}{sin\ 42} → b=\frac {22 × sin\ 42 } {sin\ 75} =\frac{22 × 0.67}{0.96}=\frac {14.74}{0.96}=15.35\ cm\)

\(\frac {22}{sin\ 75}= \frac {c}{sin\ 63} → c=\frac {22 × sin\ 63 } {sin\ 75} =\frac{22 × 0.9}{0.96}=\frac {19.8}{0.96}=20.62\ cm\)

Exercises for the Law of Sines

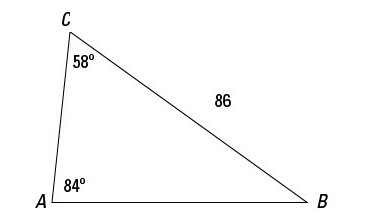
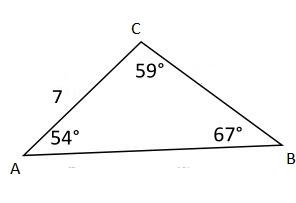
Find the side of c in the ABC triangle.

1.

2.

3.

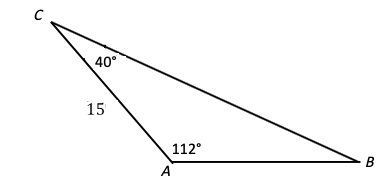
1. \(\color{blue}{73.33}\)
2. \(\color{blue}{6.51}\)
3. \(\color{blue}{20.53}\)