How to Graph the Sine Function?

A step-by-step guide to graph the sine function

The sine of an angle can be defined as the ratio of the length of the perpendicular to the length of the hypotenuse in a right triangle. The value of the sine function shows the angle between the base and the hypotenuse of a right triangle.

To graph the sine function, we plot a portion of the graph using the subset of real numbers in the interval $0\le x\:\le \:2\pi$. We know that:

Now, we plot the points whose coordinates are given in the table.

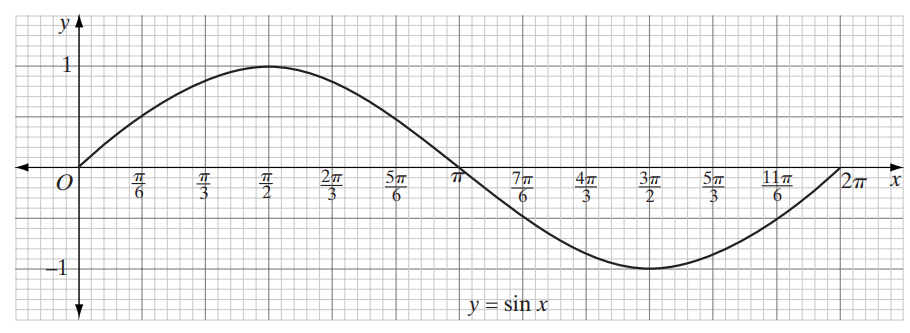
We can see how $x$ and $y$ change by using the graph:

• By increasing $x$ from $0$ to $\frac{\pi }{2}$, $y$ increases from $0$ to $1$.
• By increasing $x$ from $\frac{\pi }{2}$ to $\pi$, $y$ decreases from $1$ to $0$.
• By increasing $x$ from $\pi$ to $\frac{3\pi }{2}$, $y$ continues to decrease from $0$ to $-1$.
• By increasing $x$ from $\frac{3\pi}{2}$ to $2\pi$, $y$ increases from $-1$ to $0$.

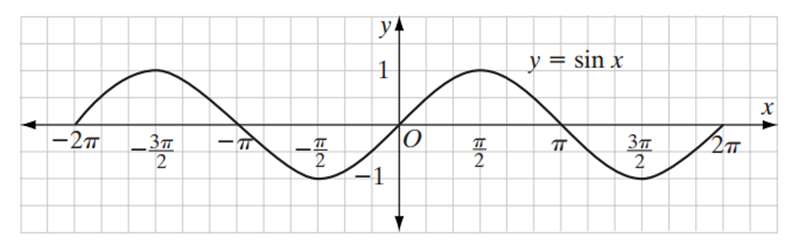
This pattern repeats itself when we plot a larger subset of the domain of the $sine$ function. For example, add to the points given above the point whose $x$-coordinates are in the interval $-2\pi \le x\le \:0$: