How to Construct Triangles? (+FREE Worksheet!)

Step by step guide to Construct triangles

A triangle is a simple closed curve or polygon which is created by three line segments. A triangle is formed when three straight lines collide with each other in such a way that if both lines intersect.

Each triangle has three sides, three angles, and three vertices.

A triangle can be drawn in the following positions with a ruler, protractor, and compass:

Having the size of two sides and the angle between them:

First, we draw an angle equal to the given angle using a conveyor. Then, using a ruler, we separate the line segment from one vertex on one of the two sides of the angle equal to the length of one of the given sides. Repeat this operation on the second side of the angle. We connect the obtained points and as a result, a triangle is drawn.

Having the size of two angles and the side between them

First, we draw a line segment equal to the length of the given side using a ruler. Then, using a conveyor, we draw one of the angles at the top of one of the two ends of the line segment. Repeat this operation on the other side of the segment and the size of the second angle of the triangle. By extending the two sides of these angles and intersecting them with each other, the third vertex of the triangle is obtained and as a result, the third triangle is drawn.

Having the size of three sides

First, we draw a line segment equal to the length of one of the given sides. Then open the opening of the compass to the size of one of the other sides and make an arc to the center of one of the two ends of the line segment. we repeat the same operation for the third side and in the other end of the line segment (open the compass opening to the size of the third side). The intersection of these two arcs is the third vertex of the triangle. A triangle is drawn by connecting the two ends of the drawn line segment to the third vertex.

Note that no triangle can be drawn with just having its three angles.

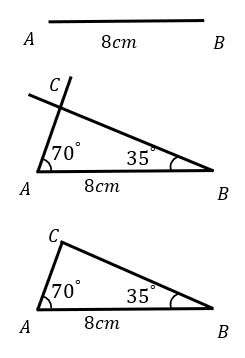
Constructing triangles – Example 1:

Construct a triangle with \(AB=8cm, ABC=35^{\circ}, BAC=70^{\circ}\)

Solution: Draw a line, \(AB=8cm\) long.

use a protractor to draw an angle, \(ABC\) of \(35^{\circ}\). Draw \(BAC=70^{\circ}\).

If necessary, extend the lines until they intersect each Other at \(C\) to form a triangle.

Erase any extra length to obtain the required triangle \(ABC\).

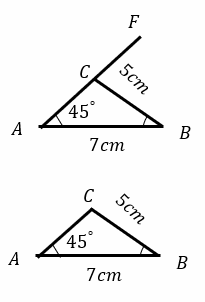
Constructing triangles – Example 2:

Use a ruler, compass, and protractor to construct a triangle \(ABC\) with \(AB=7cm, {\angle}BAC=45^{\circ}\) and \(BC=5cm\).

Solution: Draw a line,\(AB, 7cm\)  long. Draw \({\angle}BAF\) of \(45^{\circ}\)

Draw an arc of radius \(5cm\) with \(B\) as the center to cut the arc \(AF\) of \(BAF\) at \(C\). Join \(B\) and \(C\).

Erase the arc and the extra length \(CF\) to obtain the required triangle \(ABC\)

Exercises for Constructing triangles

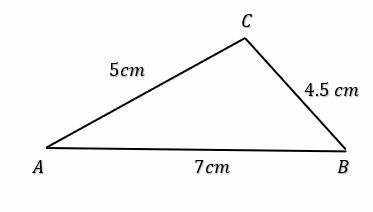
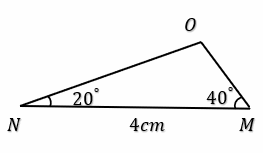
Construct each triangle by the given information.

1. \(\color{blue}{AB=7cm, AC=5cm, BC=4.5cm}\)
2. \(\color{blue}{MN=4cm, {\angle}ONM=20^{\circ}, {\angle}OMN=40^{\circ}}\)

1)

2)