How to Find the Axis of Symmetry of Quadratic Functions?
TL;DR: Every parabola has a mirror line running straight down its middle — the axis of symmetry — and it splits the curve into two identical halves. Spotting it depends on which form your quadratic is in. In standard form, the axis sits at x equals negative b over 2a. In vertex form, it's even easier: x equals h, the same h that's right there in the equation. Identify the form, plug into the right shortcut, done.
Key takeaways:
- Every parabola has an axis of symmetry - a vertical line through its vertex.
- Standard form \(f(x)=ax^2+bx+c\): axis is \(x=-\frac{b}{2a}\).
- Vertex form \(f(x)=a(x-h)^2+k\): axis is \(x=h\) (read straight off the formula).
- The vertex sits on the axis of symmetry - they share the same \(x\)-coordinate.
- If you know two points with the same \(y\)-value on the parabola, the axis is halfway between their \(x\)-coordinates.
The axis of symmetry is a straight line that makes the shape of the object symmetrical. In this step-by-step guide, you learn more about the definition of the axis of symmetry and how to find the axis of symmetry of quadratic functions.
Related Topics
A step-by-step guide to finding the axis of symmetry of quadratic functions
The axis of symmetry is a straight line that makes the shape of the object symmetrical. The axis of symmetry creates precise reflections on each of its sides.
It can be horizontal, vertical, or lateral. If we fold and unfold an object along the axis of symmetry, its two sides are the same.
Axis of symmetry of a parabola
A parabola has one line of symmetry. The axis of symmetry is a straight line that divides a parabola into two symmetrical parts.
A parabola can be in four forms. It can be horizontal or vertical, facing left or right. The axis of symmetry determines the shape of the parabola.
- If the axis of symmetry is vertical, the parabola is vertical (opens up/down).
- If horizontal, the parabola is horizontal (opens left/right).
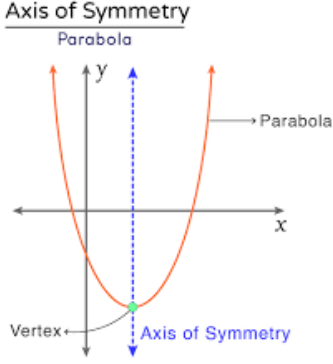
Note: The axis of symmetry, which is horizontal, has a zero slope, and the axis of symmetry, which is vertical, has an undefined slope.
Axis of symmetry equation
The vertex is the point that intersects the axis of parabola symmetry. This is the key to determining its equation.
If a parabola opens up or down, the axis of symmetry is vertical, and in this case, its equation is the vertical line that passes through its vertex.
If a parabola opens to the right or left, the axis of symmetry is horizontal and its equation is the horizontal line that passes through its vertex. That’s mean:
- The axis of symmetry of the parabola whose vertex is \((h, k)\) and opens up/down is \(x = h\).
- The axis of symmetry of the parabola whose vertex is \((h, k)\) and opens to the left/right is \(y = k\).
Axis of symmetry formula
The equation of the axis of symmetry can be shown when a parabola is in two forms:
Standard form:
The quadratic equation in standard form is, \(y = ax^2+ b x+c\), where \(a, b,\) and \(c\) are real numbers. Here, the axis of the symmetry formula is:
\(\color{blue}{x=-\frac{b}{2a}}\)
Vertex form:
The quadratic equation in vertex form is, \(y = a(x-h)^2+ k\), where \((h, k)\) is the vertex of the parabola. Here, the axis of the symmetry formula is:
\(\color{blue}{x = h}\)
Axis of Symmetry of Quadratic Functions – Example 1:
Find the axis of symmetry of the quadratic equation \(y=x^2-6x+2\).
Solution: Use this formula to find the axis of symmetry: \(x=-\frac{b}{2a}\)
\(x=-\frac{(-6)}{2(1)}\)
\(x=3\)
Recommended EffortlessMath Books
For a workbook that walks through quadratics, parabolas, and every related skill, the Algebra II for Beginners builds these ideas step by step with worked examples. If you’re prepping for calculus, the Pre-Calculus for Beginners extends the same quadratic ideas to function transformations and conic sections.
Frequently Asked Questions
What’s the axis of symmetry of a parabola?
A vertical line that splits the parabola into two mirror-image halves. It always passes through the vertex (the highest or lowest point). For a parabola opening up or down, the axis is vertical and has the form \(x=\) (some number).
What’s the formula for standard form?
For \(f(x)=ax^2+bx+c\), the axis is \(x=-\frac{b}{2a}\). The formula comes from completing the square – it’s the \(x\)-coordinate of the vertex, which is also where the axis sits. Memorize this; it’s used constantly.
What’s the formula for vertex form?
For \(f(x)=a(x-h)^2+k\), the axis is \(x=h\). Read it straight off the equation – no calculation needed. Vertex form is the easiest form for finding the axis (and the vertex). Watch the sign: \(f(x)=(x+2)^2-3\) has \(h=-2\), not 2.
Walk through a standard form example?
For \(f(x)=3x^2-12x+7\), \(a=3\) and \(b=-12\). Axis: \(x=-\frac{-12}{2(3)}=\frac{12}{6}=2\). The vertex sits at \(x=2\); plug back in to find \(y\): \(f(2)=3(4)-12(2)+7=12-24+7=-5\). So vertex is \((2,-5)\) and axis of symmetry is the vertical line \(x=2\). The parabola opens upward (\(a>0\)), so the vertex is a minimum.
Walk through a vertex form example?
For \(f(x)=-2(x-5)^2+8\), the axis is \(x=5\). The vertex is \((5,8)\) – read directly from the form. The \(-2\) in front tells you the parabola opens down (it’s a maximum, not a minimum). Vertex form is the cleanest way to express a parabola.
What if the parabola is in factored form?
Average the roots. \(f(x)=(x-2)(x-8)\) has roots at \(x=2\) and \(x=8\). Axis is \(x=\frac{2+8}{2}=5\). The vertex’s \(x\)-coordinate is 5; plug back in to get the vertex’s \(y\)-coordinate: \(f(5)=(3)(-3)=-9\). Vertex is \((5,-9)\).
Can the axis be a horizontal line?
Only if the parabola opens left or right (a sideways parabola of the form \(x=ay^2+by+c\)). For typical \(y=ax^2+\ldots\) functions, the parabola opens up or down and the axis is vertical (\(x=\) constant). Sideways parabolas are common in conic sections units.
Why does \(x=-\frac{b}{2a}\) work?
It comes from completing the square. Rewrite \(ax^2+bx+c\) as \(a(x+\frac{b}{2a})^2+c-\frac{b^2}{4a}\). That’s vertex form with \(h=-\frac{b}{2a}\). So the axis is at \(x=-\frac{b}{2a}\). Calculus students can also get this by setting \(f'(x)=0\).
How do I use symmetry to find a missing point?
If you know two points on the parabola with the same \(y\)-value, the axis is halfway between their \(x\)-coordinates. If a parabola passes through \((1,5)\) and \((7,5)\), the axis is \(x=4\). Useful for sketching or finding the vertex when you only have a graph.
Where does the axis of symmetry show up on tests?
Algebra I, Algebra II, and Pre-Calc tests; the SAT, ACT, GED, HiSET, and most state tests. Typical problems: find the axis given a quadratic; find the vertex (which sits on the axis); find a missing point using symmetry; identify the equation of a parabola from a graph.
Related EffortlessMath Lessons
If a topic on this page feels rusty, these short lessons go deeper:
Related to This Article
More math articles
- Utah RISE Grade 4 Math Free Worksheets: Printable Grade 4 Math Practice, Answers Included
- 49 Printable Tennessee TCAP Grade 3 Math Worksheets — Free Download with Step-by-Step Keys
- Full-Length ISEE Lower Level Math Practice Test
- The Best Grade 8 Math Book for Ohio Students
- FTCE Math Practice Test Questions
- Free Grade 5 English Worksheets for Oregon Students
- FREE 8th Grade PARCC Math Practice Test
- Full-Length 6th Grade ACT Aspire Math Practice Test
- Decimals Demystified: From Standard Form to Expanded Form with Fractions
- FREE Pre-Algebra Math Practice Test
What people say about "How to Find the Axis of Symmetry of Quadratic Functions? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.