Relationship Between Sides and Angles in a Triangle

By the end of this article, you will have a clear understanding of how to find and apply this relationship in various problem-solving situations.

A step-by-step guide to finding the relationship between sides and angles in a triangle

In a triangle, the sum of the measures of the three angles is always 180 degrees. This means that if you know the measures of two of the angles, you can find the measure of the third angle by subtracting the sum of the other two angles from 180 degrees.

Additionally, there is a relationship between the lengths of the sides of a triangle and the measures of the angles opposite those sides. Specifically, the longest side of a triangle is always opposite the largest angle, and the smallest side is always opposite the smallest angle.

For example, if you have a triangle with sides of lengths 5, 8, and 10, you can determine which angle is the largest and which angle is the smallest. The largest angle will be opposite the longest side (10), and the smallest angle will be opposite the shortest side (5). You can use this relationship to help you find missing angles or side lengths in a triangle if you know the measures of some of the other angles or side lengths.

Angle-Side Relationships in a triangle:
The biggest side is opposite the biggest angle and vice versa
The smallest side is opposite the smallest angle and vice versa.
An isosceles triangle is one that has 2 equal side lengths. The opposite angles of these two identical sides are similarly equal.
In a triangle, the sum of any of the two sides must be higher than the 3rd side.

Relationship Between Sides and Angles in a Triangle – Example 1

Find the smallest side of the triangle.

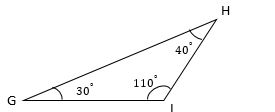
Solution:
Since, \(30^°<40^°<110^°, ∡G<∡H<∡I\), their opposite sides are in the same order, from smallest to largest: (IH) ̅\(<\)(IG) ̅\(<\)(HG) ̅
So, the smallest side is (IH) ̅.

Relationship Between Sides and Angles in a Triangle – Example 2

Find the smallest angle of the triangle.

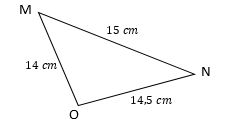
Solution:
Since \(14<14.5<15\), (MO) ̅\(<\)(ON) ̅\(<\)(MN) ̅, their opposite angles are in the same order, from smallest to largest: \(∡O<∡N<∡M\)
So, \(∡O\) is the smallest angle