Special Right Triangles
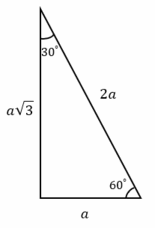
Special Right Triangles – Example 2:
Exercises for Special Right Triangles
Find the value of x and y in each triangle.
1-
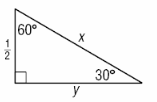
2-
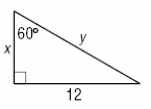
3-
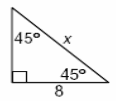
4-
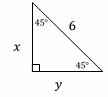
5-
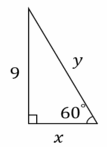
6-
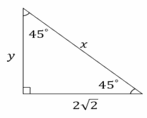
- \(\color{blue}{x=1,y=\frac{\sqrt{3}}{2}}\)
- \(\color{blue}{x=4\sqrt{3},y=8\sqrt{3}}\)
- \(\color{blue}{x=8\sqrt{2}}\)
- \(\color{blue}{x=3\sqrt{2},y=3\sqrt{2}}\)
- \(\color{blue}{x=3\sqrt{3},y=6\sqrt{3}}\)
- \(\color{blue}{x=4\,y=2\sqrt{2}}\)
The Absolute Best Book for the Algebra Test
Original price was: $29.99.$19.99Current price is: $19.99.
Original price was: $109.99.$54.99Current price is: $54.99.
Related to This Article
More math articles
- Geometry Puzzle – Challenge 60
- Citing Text Evidence in Grade 4: How to Move from Vague Answers to Clear Explanations
- Best tools for Online teachers
- Geometry Puzzle – Challenge 70
- The Best Algebra 1 Book for Wyoming Students
- FREE Pre-Algebra Math Practice Test
- Tips for Preparing Students for Math Competitions
- Free Grade 5 English Worksheets for New Mexico Students
- Classification and Biodiversity: A Beginner’s Guide
- How Political Events Shape Ideology
What people say about "Special Right Triangles - Effortless Math"?
No one replied yet.