How to Calculate Cylinder Volume and Surface Area? (+FREE Worksheet!)
In this blog post, you learn how to find the volume and surface area of cylinders by using the volume and surface area formula.
Related Topics
- How Calculate the Area of Trapezoids
- How to Find the volume and surface area of Rectangular Prisms
- How to Solve Triangles Problems
- How to Find Volume and Surface Area of Cubes
- How to Find the Perimeter of Polygons
Step by step guide to calculating Cylinders volume and surface area
- A cylinder is a solid geometric figure with straight parallel sides and a circular or oval cross section.
- Volume of Cylinder Formula \(= π\) (radius)\(^2 × \) height, \( π = 3.14\)
- The surface area of a cylinder \(=2πr^2+2πrh\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Cylinder Volume and Surface Area – Example 1:
Find the volume and Surface area of the follow Cylinder.
Solution:
Use volume formula: Volume \(= π\) (radius)\(^2 × \) height, \((r=2 cm , h=8 cm\))
Then: Volume \(=π(2)^2×8= 4π×8=32π\)
\(π=3.14\) then: Volume \(=32π=32 × 3.14 = 100.48\) \(cm^3 \)
Use surface area formula: Surface area \(=2πr^2+2πrh\)
Then: \(=2π(2)^2+2π(2)(8)=2π(4)+2π(16)=8π+32π=40π\)
\(π=3.14\) then: Surface area \(=40×3.14=125.6\) \(cm^2\)
The Best Book to Help You Ace Pre-Algebra
Cylinder Volume and Surface Area – Example 2:
Find the volume and Surface area of the follow Cylinder.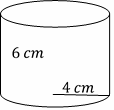 
Solution:
Use volume formula: Volume \(= π\) (radius)\(^2 × \) height, \((r=4 cm , h=6 cm\))
Then: Volume \(=π(4)^2×6= 16π×6=96π\)
\(π=3.14\) then: Volume \(=96π=96 × 3.14=301.44\) \(cm^3 \)
Use surface area formula: Surface area \(=2πr^2+2πrh\)
Then: \(=2π(4)^2+2π(4)(6)=2π(16)+2π(24)=32π+48π=80π\)
\(π=3.14\) then: Surface area \(=80×3.14=251.2\) \(cm^2\)
Exercises for Calculating Cylinder Volume and Surface Area
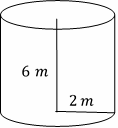
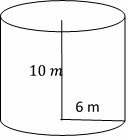
Find the volume of each Cylinder. Round your answer to the nearest tenth. \((\pi=3.14)\)
Download Cylinder Worksheet
- \(\color{blue}{75.4 \ m^3}\)
- \(\color{blue}{1,130.4 \ m^3}\)
- \(\color{blue}{1,808.6 \ m^3}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- Top 10 CLEP College Algebra Practice Questions
- ASTB Math Formulas
- How to Find the Volume and Surface Area of a Triangular Prism?
- The Ultimate 6th Grade SOL Math Course (+FREE Worksheets)
- Top 10 Free Websites for SHSAT Math Preparation
- Why Learning Styles are a Myth?
- Evaluating Variables and Expressions
- How to Find Equation of a Circle? (+FREE Worksheet!)
- 7th Grade SBAC Math Practice Test Questions
- 5th Grade NHSAS Math Worksheets: FREE & Printable
What people say about "How to Calculate Cylinder Volume and Surface Area? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.