How to Find Volume and Surface Area of Cubes? (+FREE Worksheet!)
Here you can learn how to find the volume and surface area of cubes using cubes volume and surface area formulas.
Related Topics
- How Calculate the Area of Trapezoids
- How to Find the volume and surface area of Rectangular Prisms
- How to Solve Triangles Problems
- How to Calculate Cylinder Volume and Surface Area
- How to Find the Perimeter of Polygons
Step-by-step guide to finding the Volume and Surface Area of Cubes
- A cube is a three-dimensional solid object bounded by six square sides.
- Volume is the measure of the amount of space inside of a solid figure, like a cube, ball, cylinder, or pyramid.
- Volume of a cube \(=\) (one side)\(^3\)
- surface area of cube \(=6×\) (one side)\(^2\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
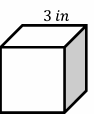
Cubes – Example 1:
Find the volume and surface area of this cube.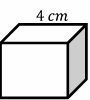 
Solution:
Use volume formula: volume \(=\) (one side)\(^3\)
Then: volume \(=\) (one side)\(^3=(4)^3=64\) \(cm^3\)
Use surface area formula: surface area of cube: \(=6\) (one side)\(^2\)
Then: surface area of cube \(=6\) (one side)\(^2=6(4)^2=6(16)=96\) \(cm^2\)
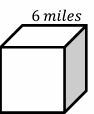
Cubes – Example 2:
Find the volume and surface area of this cube.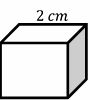 
Solution:
Use volume formula: volume \(=\) (one side)\(^3\)
Then: volume \(=\) (one side)\(^3=(2)^3=8\) \(cm^3\)
Use surface area formula: surface area of cube: \(=6\) (one side)\(^2\)
Then: surface area of cube \(=6\) (one side)\(^2=6(2)^2=6(4)=24\) \(cm^2\)
Exercises for Finding Volume and Surface Area of Cubes
The Best Book to Help You Ace Pre-Algebra
Find the volume of each cube.
Download Cubes Worksheet
- \(\color{blue}{8 \ ft^3}\)
- \(\color{blue}{125 \ m^3}\)
- \(\color{blue}{27 \ in^3}\)
- \(\color{blue}{216 \ miles^3}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- 7th Grade PARCC Math FREE Sample Practice Questions
- What Skills Do I Need for the CHSPE Math Test?
- 7 Easy Tips to Make Math Less Complicated
- Full-Length TASC Math Practice Test-Answers and Explanations
- How to Find Data Distribution
- 10 Most Common 6th Grade FSA Math Questions
- HL Congruence: The Special Case of Right Triangles
- Top 10 Tips to Overcome HSPT Math Anxiety
- The Rules of Integral: Complex Subject Made Easy
- Equivalent Rates
What people say about "How to Find Volume and Surface Area of Cubes? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.