Volume of Cubes

Cube’ is a \(3D\) solid object having 6 square faces as well as all of the sides of a cube are equal in length. It’s also known as a regular hexahedron and it is one of the \(5\) platonic solids.

The shape comprises \(6\) square faces, \(8\) vertices, and \(12\) edges.

The length, breadth, and height equal the equal measurement in a cube since the \(3D\) figure is a square with all sides equal.

Related Topics

• How to Find the Volume of Spheres?
• How to Find the Volume of Cones and Pyramids?
• How to Calculate Cylinder Volume and Surface Area?
• How to Find the volume and surface area of Rectangular Prisms?

In a cube, its faces share a commonplace boundary known as the edge which is believed to be the bounding line of its edge.

The structure is distinct with each of the faces being linked to \(4\) vertices as well as \(4\) edges, vertex linked with \(3\) edges and \(3\) faces, and the edges are in touch with \(2\) faces and \(2\) vertices.

The characteristics are:

• Cubes have twelve edges, six faces, and eight vertices.
• All the cube faces are shaped like a square so the length, breadth, and height are equal.
• The angles in-between any \(2\) faces or surfaces equal \(90°\).
• Opposite planes or faces of a cube are parallel to one another.
• The cube’s opposite edges are parallel to one another.
• Each cube face meets the additional \(4\) faces.
• Each cube vertices meets the \(3\) faces and \(3\) edges.

The volume of a Cube Utilizing Edge Length

The measurement of all a cube’s sides is equal, so we simply need to understand \(1\) side to determine the cube’s volume. The steps for calculating the cube’s volume utilizing the side’s length are here,

• Step one: Note the length of the cube’s side.
• Step one: Utilize the formula for calculating the volume utilizing the side’s length: Cube volume \(=\) \((side)^3\).
• Step three: Convey the final response along with the unit (cubic units) to correspond to the given volume.

The volume of Cube Utilizing Diagonal

Given a diagonal, you would be able to complete the steps provided underneath to determine a cube’s volume.

• Step one: Note the size of the diagonal of a particular cube.
• Step two: Use the formula to locate its volume utilizing diagonal:\(\frac{\sqrt{3×(diagonal)^3}}{9}\)
• Step three: Convey the achieved outcome via cubic units.

The volume of Cubes – Example 1:

Find the volume of the cube.

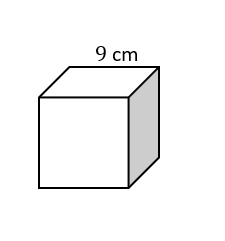
Solution:

The formula for the volume of the cube will be as follows: Volume of a cube\(=\) Width \(×\) Length \(×\) Height. If we consider each side of cube \(9\) then the volume of the cube will be : \(9 × 9 × 9=729\) \(cm^3\)

The volume of Cubes – Example 2:

Find the volume of a cube with a length of \(10\) meters.

Solution:

Volume of a cube\(=\) Width \(×\) Length \(×\) Height. So, volume of a cube\(= 10 × 10 × 10= 1000\) \(m^3\)

Exercises for Volume of Cubes

Find the volume of each cube.

1)

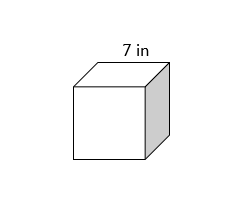
2)

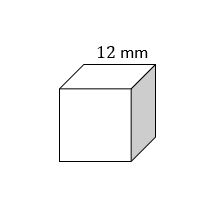
Answers

• \(\color{blue}{343in^3}\)
• \(\color{blue}{1,728mm^3}\)