How to Find the Scale Factor of a Dilation?
TL;DR: The scale factor of a dilation is the ratio of any image length to its corresponding original length: \(k = \dfrac{\text{image}}{\text{preimage}}\). If \(|k| > 1\), the figure enlarges; if \(0 < |k| < 1\), it shrinks; negative \(k\) flips it through the center.
Key takeaways:
- Scale factor formula: \(k = \dfrac{\text{image length}}{\text{preimage length}}\).
- \(|k| > 1\): enlargement (figure gets bigger).
- \(0 < |k| < 1\): reduction (figure gets smaller).
- Negative \(k\): flip through the center plus a size change.
- Distances from the center scale by \(k\); shape and angles stay the same.
Dilation is possible using the scale factor, which helps to increase or decrease the size of the object. A scale factor is a number by which the size of any shape or geometric figure can be changed relative to its original size. For additional educational resources,.
Related Topics
Step by step guide to finding the scale factor of a dilation
Dilation is the process of resizing or transforming an object. It is a transformation that makes the objects smaller or larger with the help of the given scale factor. The new figure that is obtained after dilation is called the image and the main image is called the pre-image. Dilation can be of two types:
- Expansion – When the size of an object is increased.
- Contraction – When the size of an object is decreased
Center of dilation
Dilation geometry has an important concept called the “center of expansion”. Dilation transforms the size of the figure which may increase or decrease. Resizing occurs from a point called the center of dilation. It is the center of dilation from which objects/shapes expand or contract. In the figure shown below, the triangle is enlarged from the center of dilation which is marked as \(R\).
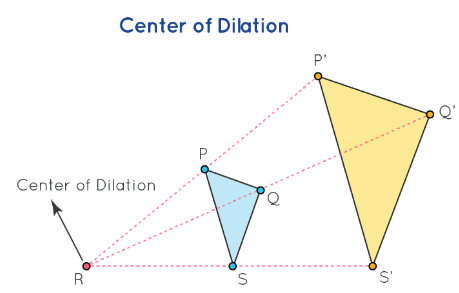
The scale factor
A scale factor is a number by which the size of any geometrical figure or shape can be changed relative to its original size. It is the ratio of the sizes of the original figure with the dilated figure.
The scale factor can be denoted by \(r\) or \(k\).
- The image is enlarged if the scale factor is more than \(1 (k > 1)\).
- The image is contracted if the scale factor is less than \(1 (0< k <1)\).
- The image remains the same if the scale factor is \(1 (k = 1)\).
Note: The magnitude of the scale factor is considered and the scale factor cannot be zero.
Scale factor formula
The scale factor can increase the size of an object or decrease the size of an object. The basic formula to find the scale factor of a dilated figure is:
\(\color{blue}{Scale\:factor\:=\:Dimension\:of\:the\:new\:shape\:\div \:Dimension\:of\:the\:original\:shape}\)
This formula can be written in another way that helps to find the dimensions of the new shape:
\(\color{blue}{Dimensions\:of\:the\:original\:shape\:×\:Scale\:factor\:=\:Dimension\:of\:the\:new\:shape}\)
Exercises for Finding the Scale Factor of a Dilation
- The length of each side of the square is \(6\) units. If the scale factor is \(3\), what will be the length of each side of the expanded square?
- Find the scale factor of the dilation.
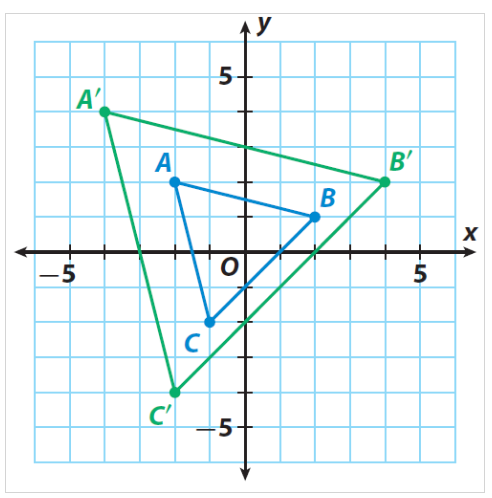
- \(\color{blue}{18}\)
- \(\color{blue}{2}\)
Recommended EffortlessMath Books
For a deeper walk through every geometry skill from the ground up, Geometry for Beginners covers angles, area, volume, triangles, and transformations with worked examples and plenty of practice. For algebra-heavy geometry topics, the companion Algebra I for Beginners ties the coordinate-plane work back to linear equations.
Frequently Asked Questions
What is a dilation?
A transformation that resizes a figure – making it bigger or smaller – while keeping its shape. Every point in the figure moves toward or away from a fixed point (the center of dilation) by the same scale factor. Angles stay the same; lengths multiply by the scale factor.
What’s the scale factor formula?
\(k = \dfrac{\text{image length}}{\text{preimage length}}\). Take any side of the new figure (image) and divide by the corresponding side of the original (preimage). This ratio is the scale factor. It’s also the ratio of any image-to-center distance over preimage-to-center distance.
What does scale factor > 1 mean?
The image is LARGER than the original – an enlargement. \(k = 2\) doubles all lengths; \(k = 3\) triples them; \(k = 1.5\) makes everything 50% bigger. Area scales by \(k^2\), so doubling the side quadruples the area.
What does scale factor < 1 mean?
The image is SMALLER than the original – a reduction. \(k = 0.5\) halves all lengths; \(k = \dfrac{1}{3}\) shrinks to a third. Area scales by \(k^2\), so halving the side leaves only a quarter of the area. Useful for scale drawings of large objects.
What about a negative scale factor?
The image is on the OPPOSITE side of the center from the original, AND scaled by \(|k|\). \(k = -1\) rotates the figure \(180^\circ\) about the center (no size change). \(k = -2\) flips through center AND doubles size. Negative scale factors aren’t common at the high-school level but show up in advanced geometry.
How do I find scale factor from coordinates?
Pick a pair of corresponding points and divide their distances from the center. If the center is the origin and a point is at \((4, 6)\) with image at \((6, 9)\), the scale factor is \(6/4 = 1.5\) (or check y: \(9/6 = 1.5\) ✓). Any non-center point works.
Walk me through an example.
Triangle \(ABC\) has side \(AB = 8\). After dilation, image triangle \(A’B’C’\) has \(A’B’ = 12\). Scale factor: \(k = 12/8 = 1.5\). This is an enlargement, since \(k > 1\). All sides of \(A’B’C’\) are 1.5 times the corresponding sides of \(ABC\), and the area is \(1.5^2 = 2.25\) times bigger.
How does the center of dilation matter?
The center is the fixed point that doesn’t move during the dilation. Every other point’s distance from the center changes by the scale factor. Moving the center changes WHERE the image lands but not its size or shape. The scale factor depends only on lengths, not on the center’s position.
How does area change under dilation?
Area scales by \(k^2\). If \(k = 3\), area becomes \(9\) times the original. If \(k = \dfrac{1}{2}\), area becomes \(\dfrac{1}{4}\) of the original. Volume of 3D figures scales by \(k^3\). This is why doubling a model’s height takes 8 times as much material for a solid replica.
Where does this skill show up?
Geometry class, SAT, ACT, and most state high-school math tests. Real-world uses: scale drawings, maps, models, blueprints, photography enlargements, and digital image scaling. Knowing how lengths, areas, and volumes scale differently is crucial for engineering, architecture, and visual design.
Related EffortlessMath Lessons
If a topic on this page feels rusty, these short lessons go deeper:
Related to This Article
More math articles
- The Rules of Integral: Complex Subject Made Easy
- Top 10 Tips to Create an ATI TEAS 7 Math Study Plan
- How to Decode Data Types
- How to Master Polynomial Functions
- Unlocking the Secrets of Triangle Angle Sum
- The Best Grade 5 ELA Practice Tests for Texas Students
- How to Make Smart Payment Methods and Financial Decisions? (+FREE Worksheet!)
- 49 Free Grade 5 Math Worksheets for Tennessee TCAP Prep, Built Around the Real Skill List
- Free Texas Grade 2 Math Worksheets
- Digital Clocks
What people say about "How to Find the Scale Factor of a Dilation? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.