How to Graph Transformation on the Coordinate Plane: Dilation?

Related Topics

• How to Graph Transformation on the Coordinate Plane: Reflection?
• How to Find Transformation: Rotations, Reflections, and Translations?
• How to Graph Transformation on the Coordinate Plane: Rotation?
• How to Graph Translations on the Coordinate Plane?

Step by step guide to graph Transformation: Dilation

A dilation is a type of transformation that creates an image that is the same shape as the original but in a different size.

In a Dilation, each point of an object is moved along a straight line. The straight line is drawn from a fixed point called the center of dilation. The distance the points move depends on the scale factor. The center of dilation is the only invariant point. The scale factor tells us how much this figure is stretched or reduced.

$Scale\space factor:$ $\frac{image\space length}{original\space length}=\frac{distance\space of \space image \space from\space center\space of\space dilation}{distance\space of\space object\space from\space center\space of\space dilation}$

Transformation: Dilation – Example 1:

Dilate the image with a scale factor of $2.5$.

Solution:

: First, find the original coordinates:

$A=(-2, -2)$ $B=(0, 2)$ $C=(2, -2)$

Next, take all of the coordinates, and multiply them by $2.5$:

$A^\prime=(-5, -5)$ $B^\prime=(0, -5)$ $C^\prime=(5, -5)$

Now, graph the new image. Since the new figure is larger and our scale factor is greater than $1$, the new image is an enlargement.

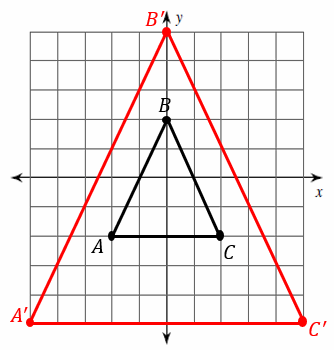
Transformation: Dilation – Example 2:

Dilate the image with a scale factor of $0.5$.

Solution:

: First, find the original coordinates:

$A=(-4, 0)$ $B=(0, 2)$ $C=(2, 0)$ $D=(-2, -4)$

Next, take all of the coordinates, and multiply them by $0.5$:

$A^\prime=(-2, 0)$ $B^\prime=(0, 1)$ $C^\prime=(1, 0)$ $D^\prime=(-1, -2)$

Now, graph the new image.

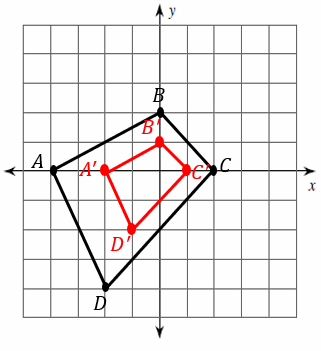
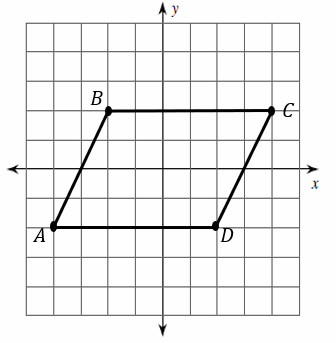
Exercises for Transformation: Dilation

Graph the image of the figure using the transformation given.

1) Dilation of $2$

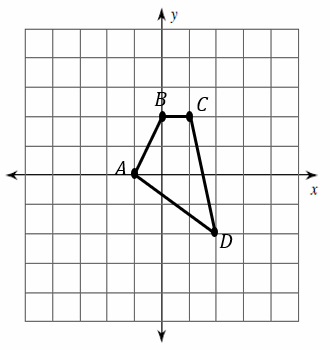
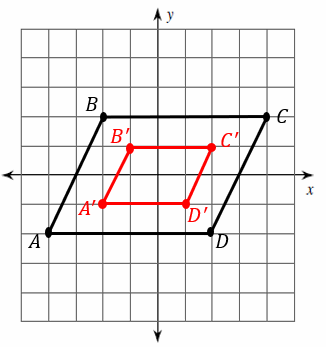
2) Dilation of $0.5$

1)

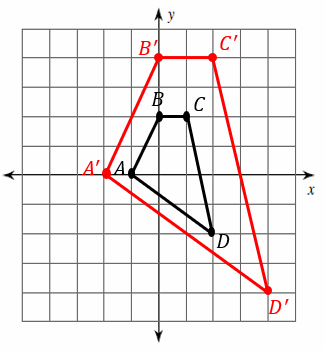
2)