How to Graph Transformation on the Coordinate Plane: Rotation?

Step by step guide to graph Transformation: Rotation

A rotation is a transformation in which the object is rotated about a fixed point. The direction of rotation can be clockwise or counterclockwise. In this case, an image and its pre-image have the same shape and size, but the pre-image may be turned in different directions

We can rotate shapes on the coordinate \(90, 180,\) or \(270\) degrees counterclockwise around the origin using three basic rules:

• For rotating a shape \(90\) degrees counterclockwise:\((x, y)→(-y, x)\)
• For rotating a shape \(180\) degrees: \((x, y)→(-x, -y)\)
• For rotating a shape \(270\) degrees counterclockwise: \((x, y)→(y, -x)\)

Remember that:

• You should be able to assume the center of rotation to be the origin when working on the coordinate plane unless otherwise stated.
• You should be able to assume that, unless otherwise stated, a positive angle of rotation rotates the figure counterclockwise and a negative angle rotates it clockwise.
• You need to be able to recognize angles of certain sizes when working with rotation. \((90^{\circ}, 180^{\circ}, 270^{\circ}, …)\)
• You must be able to understand the directionality of a unit circle. (the circle with a radius length of \(1\) unit)
• You must know that rotation on a coordinate grid is considered to be counterclockwise unless otherwise stated.

Transformation: Rotation – Example 1:

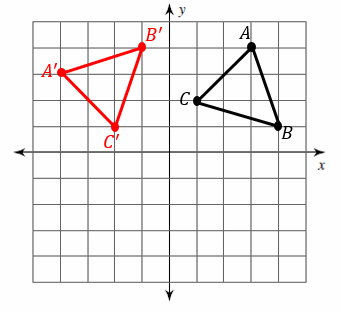
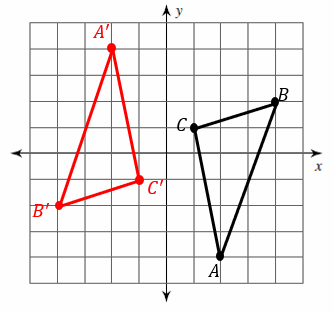
Triangle \(ABC\) has vertices \(A=(3, 4), B=(4, 1), C=(1, 2)\). Graph triangle \(ABC\) and its image after a rotation of \(90^{\circ}\) about the origin.

Solution:

The rule for rotating a shape 90 degrees is \((x, y)→(-y, x)\)

\(A=(3, 4)→A^\prime=(-4, 3)\)

\(B=(4, 1)→B^\prime=(-1, 4)\)

\(C=(1, 2)→C^\prime=(-2, 1)\)

Graph Triangle \(ABC\) and its image \(A^\prime B^\prime C^\prime\).

Transformation: Rotation – Example 2:

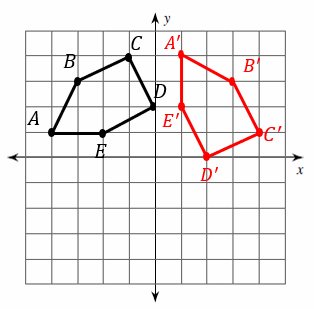
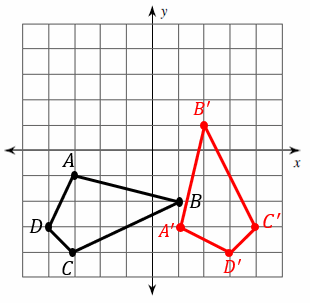
Graph the image of the figure after a rotation of \(270^{\circ}\) about the origin.

Solution:

The rule for rotating a shape \(270\) degrees is \((x, y)→(y, -x)\)

\(A=(-4, 1)→A^\prime=(1, 4)\)

\(B=(-3, 3)→B^\prime=(3, 3)\)

\(C=(-1, 4)→C^\prime=(4, 1)\)

\(D=(0, 2)→D^\prime=(2, 0)\)

\(C=(-2, 1)→C^\prime=(1, 2)\)

Graph the figure \(ABCDE\) and its image \(A^\prime B^\prime C^\prime D^\prime E^\prime\).

Exercises for Transformation: Rotation

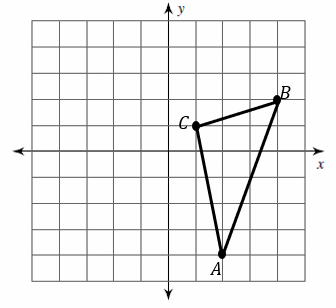
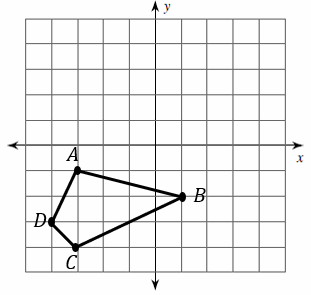
Graph the image of the figure using the transformation given.

1.\(\color{blue}{Rotation 180^{\circ}}\)

2.\(\color{blue}{Rotation 90^{\circ}}\)