Perimeters and Areas of Rectangles
In this article, we will learn how to calculate the perimeter and area of a rectangle
Rectangles are closed \(2\)-dimensional figures having \(4\) sides. The opposing sides of rectangles are identical as well as parallel to one another as well and all the rectangle’s angles are equal \(90°\).
A few of the vital characteristics are rectangles shown here.
- Rectangles are quadrilaterals.
- The opposing sides’ rectangles are identical and parallel to one another.
- The inner angle of a rectangle at each of the vertexes equals \(90°\).
- The total of all inner angles equals \(360°\).
- Its diagonals bisect one another.
- The diagonals’ length is identical.
- The diagonals’ length can be achieved via the Pythagoras theorem. The diagonal’s length with sides a and b is, diagonal = \(\sqrt{(a^2+b^2})\).
- Because the rectangle’s sides are parallel, it’s additionally known as a parallelogram.
- Every rectangle is a parallelogram, however, not every parallelogram is a rectangle.
The Absolute Best Book for 4th Grade Students
Related Topics
- Quadrilaterals and Rectangles
- Perimeters and Areas of Squares
- How to Find the Perimeter of Polygons?
- How to Find the Area and Circumference of Circles?
Rectangle’s area:
A rectangle’s area is the number of unit squares which is able to fit into a rectangle. So, the space inhabited by the rectangle is the rectangle’s area.
The formula to get a rectangle’s area where the length and width are ‘\(l\)’ and ‘\(w\)’ individually is the outcome of its length and width, so:
Area of a Rectangle \(= (l × w)\)
A Perfect Book for Grade 4 Math Word Problems!
Rectangle’s perimeter
A rectangle’s perimeter is the length of the complete rectangle’s boundary. It may be taken as the calculation of the complete measurement of the rectangle’s length and width and it’s shown in linear units such as inches, centimeters, etc.
The formula to get the perimeter, ‘\(P\)’ of a rectangle where the width and length are ‘\(w\)’ and ‘\(l\)’ respectively is \(2(l + w)\).
Formula for the Perimeter of a Rectangle \(= 2 (Length + Width)\)
Perimeters and Areas of Rectangles – Example 1:
Find the area and perimeters of a rectangle with \(12\) cm length and \(6\) cm width
Solution:
The formula to get a rectangle’s area = Length × Width. So, the rectangle’s area is \(12 × 6=72\)
The formula for the perimeter of a rectangle = \(2\) (Length + Width). So, the perimeter of a rectangle \(= 2(12+6)=36\)
Perimeters and Areas of Rectangles – Example 2:
Find the area and perimeter of the rectangle
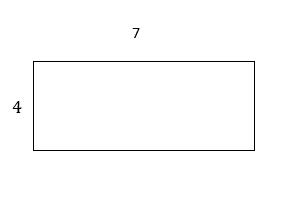
Solution:
The formula to get a rectangle’s area = Length × Width. So, the rectangle’s area is \(7 × 4=28\)
The formula for the perimeter of a rectangle = \(2\) (Length + Width). So, the perimeter of a rectangle \(= 2(7+4)=22\)
Exercises for Perimeters and Areas of Rectangles
Find the perimeter and area of rectangles
1)
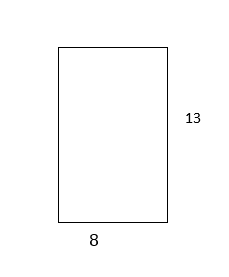
2)
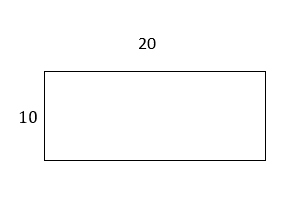
Answers
- \(\color{blue}{42,104}\)
- \(\color{blue}{60,200}\)
The Best Math Books for Elementary Students
Related to This Article
More math articles
- Tri-Fractional Operations: How to Add and Subtract Three Fractions with Different Denominators
- Top 10 Tips You MUST Know to Retake the CLEP College Math
- 5th Grade FSA Math Practice Test Questions
- 4th Grade MAP Math Practice Test Questions
- How to Balance the Scales: Inequalities with Addition and Subtraction of Mixed Numbers
- How Is the SHSAT Test Scored?
- Top 10 Grade 3 Math Books: Inspiring Young Mathematicians to Explore
- How is the GED Math Scored?
- How to Graph Trigonometric Functions?
- 4th Grade IAR Math Practice Test Questions
What people say about "Perimeters and Areas of Rectangles - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.