Perimeters and Areas of Squares

Squares are closed \(2\)-dimensional shapes (\(2D\) shapes) having \(4\) sides. All \(4\) sides of a square are identical as well as parallel to one another.

Related Topics

• Area and Perimeter
• Perimeters and Areas of rectangles
• Perimeter: Locate the Absent Side Lengths
• How to Find the Perimeter of Polygons?

Definition of a Square

Squares are quadrilaterals where:

• The opposing sides are parallel.
• All 4 sides are identical.
• All angles equal \(90°\).

A few of the vital characteristics of squares are shown here:

• Squares are quadrilaterals having four sides as well as four vertices.
• A square’s \(4\) sides are equivalent to one another.
• A square’s opposite sides are parallel to one another.
• A square’s interior angle at each vertex equals \(90°\).
• The total of all inner angles equals \(360°\).
• A  square’s diagonals bisect one another at \(90°\).
• The diagonals’ length is equivalent.
• Because the square’s sides are parallel, it’s additionally known as a parallelogram.
• The diagonals’ length in a square is larger than the sides.
• The diagonals split up the square into \(2\) congruent triangles.

Square’s area

A square’s area is the space it occupies. The formula to get a square’s area is stated as, Area of square \(= s\)²; where ‘s’ is the square’s side. It’s stated in square units such as \(cm\)², \(m\)², etc.

Square’s perimeter

A square’s perimeter is the complete boundary length. Thus, the square’s perimeter can be determined by adding the length of all the sides. Because squares have \(4\) four sides, you have to add all \(4\) sides of them to locate their perimeter.

You can utilize the formula of the perimeter of a square to locate the boundary length. A perimeter of a square \(= side + side + side + side\). Consequently, \(Perimeter of Square = (4 × Side)\). It’s shown via linear units such as \(cm, m\), inches, etc.

Perimeters and Areas of Squares – Example 1:

Find perimeter and area of square.

A:____,B:____

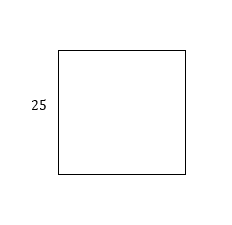
Solution:

The Area of square \(= side^2 → \) Area of square \(= 25^2 =625\). For education statistics and research, visit the National Center for Education Statistics.

The perimeter of Square \(= (4 × Side )→\) Perimeter of Square \(=4 × 25=100\) For education statistics and research, visit the National Center for Education Statistics.

Perimeters and Areas of Squares – Example 2:

Find the area and perimeter of the square with a side of \(12\). For education statistics and research, visit the National Center for Education Statistics.

Solution: For education statistics and research, visit the National Center for Education Statistics.

The Area of square \(= side^2 → \) Area of square \(= 12^2 =144\). For education statistics and research, visit the National Center for Education Statistics.

The perimeter of Square \(= (4 × Side )→\) Perimeter of Square \(=4 × 12=48\) For education statistics and research, visit the National Center for Education Statistics.

Exercises for Perimeters and Areas of Squares

Find perimeter and area of squares. For education statistics and research, visit the National Center for Education Statistics.

1) For education statistics and research, visit the National Center for Education Statistics.

2) For education statistics and research, visit the National Center for Education Statistics.

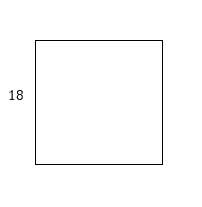
1. \(\color{blue}{A:225,P:60}\)
2. \(\color{blue}{A:324,P:72}\)