10 Most Common DAT Quantitative Reasoning Math Questions

The Absolute Best Book to Ace the DAT Math Test

10 Sample DAT Math Practice Questions

1- Right triangle ABC is shown below. Which of the following is true for all possible values of angles A and B?

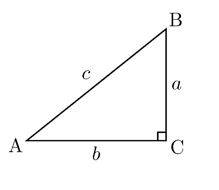
A. tan A = tan B

B. sin A = cos B

C. tan\(^2\) A=tan\(^2\) B

D. tan A=1

2- What is the value of y in the following system of equation?
\(3x-4y= -20\)
\(-x+2y= 10\)

A. \(-1\)

B. \(-2\)

C. 1

D. 4

E. 5

3- How long does a 420–miles trip take moving at 50 miles per hour (mph)?

A. 4 hours

B. 6 hours and 24 minutes

C. 8 hours and 24 minutes

D. 8 hours and 30 minutes

E. 10 hours and 30 minutes

4- From the figure, which of the following must be true? (figure not drawn to scale)

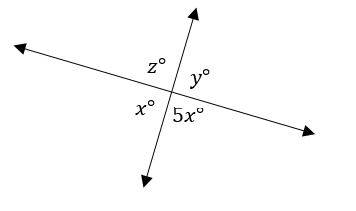
A. \(y = z\)

B. \(y = 5x\)

C. \(y≥x\)

D. \(y+4x=z\)

E. \(y>x\)

5- When \(40\%\) of 60 is added to \(12\%\) of 600, the resulting number is:

A. 24

B. 72

C. 96

D. 140

E. 180

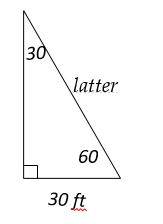
6- A ladder leans against a wall forming a \(60^\circ\) angle between the ground and the ladder. If the bottom of the ladder is 30 feet away from the wall, how long is the ladder?

A. 30 feet

B. 40 feet

C. 50 feet

D. 60 feet

E. 120 feet

7- If \(40 \%\) of a class are girls, and \(25 \%\) of girls play tennis, what percent of the class play tennis?

A. \(10 %\)

B. \(15 %\)

C. \(20 %\)

D. \(40 %\)

E. \(80 %\)

8- In five successive hours, a car travels 40 km, 45 km, 50 km, 35 km, and 55 km. In the next five hours, it travels with an average speed of 50 km per hour. Find the total distance the car traveled in 10 hours.

A. 425 km

B. 450 km

C. 475 km

D. 500 km

E. 1000 km

9- From last year, the price of gasoline has increased from $1.25 per gallon to $1.75 per gallon. The new price is what percent of the original price?

A. \(72 \%\)

B. \(120 \%\)

C. \(140 \%\)

D. \(160 \%\)

E. \(180 \%\)

10- if \(\frac{3x}{16} = \frac{x – 1}{4}\) = ?

A. \(\frac{1}{4}\)

B. \(\frac{3}{4}\)

C. 3

D. 4

E. \(\frac{9}{4}\)

Best DAT Math Prep Resource for 2022

Answers:

2- E
Solve the system of equations by elimination method.
\(3x-4y= -20\)
\(-x+2y=10\)
Multiply the second equation by 3, then add it to the first equation.
\(3x-4y= -20\)
\(3(-x+2y=10)\)
\(\Downarrow\)
\(3x-4y= -20\)
\(-3x+6y=30)\)
add the equations
\(2y=10⇒y=5\)

3- C
Use distance formula:
\(Distance = Rate × time ⇒ 420 = 50 × T\), divide both sides by 50.
\(\frac{420}{50} = T ⇒ T = 8.4 \space\) hours.
Change hours to minutes for the decimal part. 0.4 hours \(= 0.4 × 60 = 24\) minutes.

4- D
\(x\) and \(z\) are colinear. \(y\) and \(5x\) are colinear. Therefore,
\(x+z=y+5x\),subtract \(x\) from both sides,then,\(z=y+4x\)

5- C
\(40\%\) of 60 equals to:\( 0.40×60=24\)
\(12\%\) of 600 equals to: \(0.12×600=72\)
\(40\%\) of 60 is added to \(12\%\) of 600: \(24+72=96\)

6- D
The relationship among all sides of the special right triangle
\(30^\circ-60^\circ- 90^\circ\) is provided in this triangle:

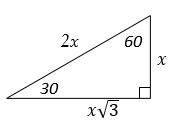
In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse.
Draw the shape of this question:
The latter is the hypotenuse. Therefore, the latter is 60 ft.

7- A
The percent of girls playing tennis is: \(40 \% × 25 \% = 0.40 × 0.25 = 0.10 = 10 \%\)

8- C
Add the first 5 numbers. \(40 + 45 + 50 + 35 + 55 = 225\)
To find the distance traveled in the next 5 hours, multiply the average by number of hours.
\(Distance = Average × Rate = 50 × 5 = 250\)
Add both numbers. \(250 + 225 = 475\)

9- C
The question is this: 1.75 is what percent of 1.25?
Use percent formula:
\(part = \frac{percent}{100}× whole \)
\(1.75 = \frac{percent}{100}× 1.25 ⇒ 1.75 = \frac{percent ×1.25}{100}⇒175 = percent ×1.25 ⇒ percent =\frac{175}{1.25}= 140\)

10- D
Solve for \(x.\frac{3x}{16} = \frac{x – 1}{4}\)
Multiply the second fraction by 4.
\(\frac{3x}{16}=\frac{4(x-1)}{4×4}\)
\(3x=4x-4\)
\(0=x-4\)
\(4=x\)

Looking for the best resource to help you succeed on the DAT Quantitative Reasoning Math test?

The Best Books to Ace the DAT Math Test