Full-Length DAT Quantitative Reasoning Practice Test-Answers and Explanations
Did you take the DAT Quantitative Reasoning Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
DAT Quantitative Reasoning Practice Test Answers and Explanations
1- Choice A is correct
Solve the system of equations by elimination method.
\(\begin{cases}2x+y=7\\4x-2y=18\end{cases}\)
\(\begin{cases}2(2x+y=7)\\4x-2y=18\end{cases}⇒\begin{cases}4x+2y= 14\\4x-2y=18\end{cases}\)⇒ add the equations
\(8x=32⇒x=4,2x+y=7⇒y=7-2(4)=7-8=-1\)
2- Choice C is correct.
100 times the number is 6.45. Let \(x\) be the number, then: \(100x=6.45\), \(x=\frac{6.45}{100}=0.0645\)
3- Choice C is correct
The area of the floor is: 6 cm \(×\) 32 cm = 192 cm, The number is tiles needed =\( 192 ÷ 12 = 16\)
4- Choice E is correct
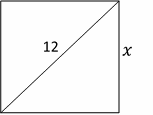
The diagonal of the square is 12. Let \(x\) be the side.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
\(x^2 + x^2 = 12^2 ⇒ 2x^2=12^2 ⇒ 2x^2 = 144 ⇒ x^2 = 72 ⇒x= \sqrt{72}\)
The area of the square is: \(\sqrt{72} ×\sqrt{72}=72\)
5- Choice E is correct
\(x=26+136=162\)
6- Choice B is correct.
By definition, the sine of an acute angle is equal to the cosine of its complement.
Since, angle A and B are complementary angles, therefore: sin A = cos B
7- Choice E is correct
To find the discount, multiply the number by (\(100\%\) – rate of discount).
Therefore, for the first discount we get: \((D) (100\% – 15\%) = (D) (0.85) = 0.85 D\)
For increase of \(22\%\): \((0.85 D) (100\% + 22\%) = (0.85 D) (1.22) = 1.037 D = 103.7\%\) of \(D\)
8- Choice D is correct
If 14 balls are removed from the bag at random, there will be one ball in the bag. The probability of choosing a red ball is 1 out of 15. Therefore, the probability of not choosing a red ball is 14 out of 15 and the probability of having not a red ball after removing 14 balls is the same.
9- Choice D is correct
\(x\) and \(2z\) are colinear. \(y\) and \(3x\) are colinear. Therefore,
\(x+2z=y+3x\), subtract \(x\) from both sides,then, \(2z=y-2x\)
10- Choice C is correct
\(45\%\) of \(30\) equals to: \(0.45×30=13.5\), \(15\%\) of \(420\) equals to: \(0.15×420=63\)
\(45\%\) of \(30\) is added to \(15\%\) of \(420\): \(13.5+63=76.5\)
11- Choice C is correct
\(12\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(12\%\) of \(x=48\) ml ⇒ \(0.12 x=48 ⇒ x=48÷0.12=400\)
12- Choice D is correct
Plug in each pair of number in the equation:
A. \((-3,2): 3(-3)-2(2)=-13\) Nope!
B. \((-1,2): 3(–1)-2(2)=-7\) Nope!
C. \((1,2): 3(1)-2(2)=-1\) Nope!
D. \((2,-1): 3(2)-2(-1)=8\) Bingo!
E. \((3,0): 3(3)-2(0)=9\) Nope!
13- Choice B is correct
The area of ∆BED is 21, then: \(\frac{6×AB}{2}=21→6×AB=42→AB=7\)
The area of ∆BDF is 32, then: \(\frac{4×BC}{2} =32→4×BC=64→BC=16\)
The perimeter of the rectangle is = \(2×(7+16)=46\)
14- Choice B is correct
\(|x+8|≤2→-2≤x+8≤2→-2-8≤x+8-8≤2-8→-10≤x≤-6\)
The Absolute Best Book to Ace the DAT Quantitative Reasoning Test
15- Choice D is correct
Use distance formula: Distance = Rate \(×\) time ⇒ 564 \(= 60 × \)T, divide both sides by 60. \(\frac{564}{60}\) = T ⇒ T = 9.4 hours. Change hours to minutes for the decimal part. 0.4 hours \(= 0.4 × 60 = 24\) minutes.
16- Choice B is correct
Write a proportion and solve for \(x⇒ \frac{3}{4}=\frac{x}{36} ⇒ 4x=3 ×36 ⇒ x=27\) ft
17- Choice D is correct
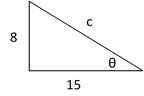
\(tanθ=\frac{opposite}{adjacent}\)
\(tanθ=\frac{8}{15}\)⇒ we have the following right triangle. Then
\(c=\sqrt{8^2+15^2}=\sqrt{64+225}=\sqrt{289}=17\)
\(cosθ=\frac{adjacent}{hypotenuse}=\frac{15}{17}\)
18- Choice C is correct
The percent of girls playing tennis is: \(65\%×20\%=0.65×0.20=0.13=13\%\)
19- Choice B is correct
Add the first 4 numbers. \(55+62+44+63=224\), To find the distance traveled in the next 4 hours, multiply the average by the number of hours. Distance = Average × Rate \(=65×4=260\), Add both numbers. \(224+260=484\)
20- Choice D is correct
The question is this: 1.82 is what percent of 1.3? Use percent formula: \(part=\frac{percent}{100}×whole\)
\(1.82 = \frac{percent}{100} × 1.3 ⇒ 1.82=\frac{percent ×1.3}{100} ⇒182=percent×1.3 ⇒ percent=\frac{182}{1.3}= 140\)
21- Choice E is correct.
Solve for \(x ⇒ \frac{5x}{18}=\frac{x-2}{3}\)⇒ Multiply the second fraction by \(6⇒ \frac{5x}{18}=\frac{6(x-2)}{6×3}\)
Tow denominators are equal. Therefore, the numerators must be equal.
\(5x=6(x-2)=6x-12, x=12\)
22- Choice E is correct
The relationship among all sides of a special right triangle
\(30^\circ -60^\circ- 90^\circ\) is provided in this triangle:
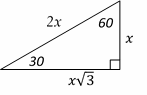
In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse.
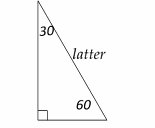
Draw the shape of this question:
The latter is the hypotenuse. Therefore, the latter is 40 ft.
23- Choice D is correct
The weight of 14 meters of this rope is: \(14×732 \space g=10,248 \space g\)
\(1 \space kg = 1000 \space g\), therefore, \(10,248 \space g÷1000=10.248 \space kg\)
24- Choice E is correct
The slop of line A is: \(m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-(-6)}{4-2}=\frac{8}{2}=4\)
Parallel lines have the same slope and only choice E \((y=4x)\) has a slope of 4.
25- Choice E is correct
When points are reflected over \(y\)-axis, the value of \(y\) in the coordinates doesn’t change and the sign of \(x\) changes. Therefore, the coordinates of point B are (4, 5).
26- Choice C is correct
The area of trapezoid is: \(\frac{(9+12)}{2}×x =42→21x=84→x=4\), \(y=\sqrt{3^2+4^2}=5\)
Perimeter is: \(4+9+5+3+9=30\)
27- Choice C is correct
Set of number that are not composite between 1 and 18: \(A = {1, 2, 3, 5, 7, 11, 13, 17}\)
Probability \(= \frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}=\frac{8}{18}=\frac{4}{9}\)
28- Choice B is correct
Check each option provided:
A. \(2 → \frac{4+6+8+12}{4}=\frac{30}{4}=7.5\)
B. \(4 → \frac{2+6+8+12}{4}=\frac{28}{4}=7\)
C. \(6 → \frac{2+4+8+12}{4}=\frac{26}{4}=6.5\)
D. \(8 → \frac{2+4+6+12}{4}=\frac{24}{4}=6\)
E. \(12 → \frac{2+4+6+8}{4}=\frac{20}{4}=5\)
29- Choice B is correct
\(0.5x=(0.2)×30→x=12→(x-4)^2=(12-4)^2=8^2=64\)
Best DAT Quantitative Reasoning Prep Resource for 2022
30- Choice D is correct.
Let the number be \(x\). Then: \(12=4\%×x→12=0.04x\), Solve for \(x→x=\frac{12}{0.04}=300\)
31- Choice C is correct
\(f(x)=2x^2-x,g(x)=x^2-6 , (f-g)(x)=f(x)–g(x)=(2x^2-x)-(x^2-6 )=2x^2-x-x^2+6=x^2-x+6\)
32- Choice A is correct
\(f(x)=-x^3-4x^2+6x+7,g(x)=-1\), then: \(f(g(x))= f(-1)=-(-1)^3-4(-1)^2+6(-1)+7=-(-1)-4(1)-6+7=1-4-6+7=-2\)
33- Choice A is correct
Plug in \(\frac{z}{5}\) for \(z\) and simplify.
\(x=\frac{8y+\frac{r}{r+1}}{\frac{6}{\frac{z}{5}}}=\frac{8y+\frac{r}{r+1}}{\frac{5×6}{z}}=\frac{8y+\frac{r}{r+1}}{5×\frac{6}{z}}=\frac{1}{5}×\frac{8y+\frac{r}{r+1}}{\frac{6}{z}}=\frac{x}{5}\)
34- Choice B is correct
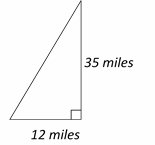
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2+b^2=c^2\)
\(12^2+35^2=c^2 ⇒ 144+1225= c^2⇒1369=c^2⇒ c=37\)
35- Choice D is correct
\(y =ab^2-3a^2 b ,a=2,b=-2\), Plug in the values of a and b in the equation: \(y=2(-2)^2-3(2)^2 (-2)=2(4)-3(4)(-2)=8+24=32\)
36- Choice A is correct
I. \(|a|<1→-1<a<1\)
Multiply all sides by \(b\). Since, \(b>0\) →\(-b<ba<b\) (it is true!)
II. Since, \(-1<a<1\), and \(a<0→-a>a^2>a\) (plug in \(−\frac{1}{2}\), and check!) (It’s false)
III. \(-1<a<1\), multiply all sdes by \(4\), then: \(-4<4a<4\)
Subtract \(5\) from all sides. Then: \(-4-5<4a-5<4-5→-9<4a-5<-1\) (It is false!)
37- Choice C is correct
\(One \space liter = 1000 \space cm^3→ 8 \space liters = 8000 \space cm^3⇒ 8000=16×5×h→h=\frac{8000}{80}=100 \space cm\)
38- Choice E is correct
\(\frac{3}{4}×120=90\)
39- Choice C is correct
\(tangent \space β= \frac{1}{cotangent \space β}=\frac{1}{1}=1\)
40- Choice E is correct
Surface Area of a cylinder \(= 2πr (r+h)\), The radius of the cylinder is \(4(8÷2)\) inches and its height is \(12\) inches. Therefore, the Surface Area of a cylinder \(=2π(4)(4+12)=128π\)
The Best Books to Ace the DAT Quantitative Reasoning Test
Related to This Article
More math articles
- What Kind of Math Learner Is Your Child?
- 6th Grade Georgia Milestones Assessment Math Worksheets: FREE & Printable
- Big Number Brainwork: How to Solve Word Problems with Large Whole Number Operations
- How to Master Integrals
- How to Prepare for the PSAT 10 Math Test?
- Which Test Is Better for You; GED, TASC, or HiSET? Find Out Now
- 7th Grade IAR Math Practice Test Questions
- How to Prepare for Math Exams: Study Tips & Tricks
- How to Factor Numbers? (+FREE Worksheet!)
- 4th Grade NYSE Math FREE Sample Practice Questions
What people say about "Full-Length DAT Quantitative Reasoning Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.