Quadrilaterals and Rectangles

Within geometry, quadrilaterals are closed shapes created by linking \(4\) points amongst which any \(3\) points are non-collinear.

Quadrilaterals have four sides, four angles, as well as four vertices.

‘Quadrilateral’ comes from a Latin term, where, ‘Quadra’ stands for \(4\) and ‘Latus’ stands for sides. All four of the sides of quadrilaterals might or might not be identical.

Related Topics

• Perimeters and Areas of Squares
• Perimeters and Areas of rectangles
• How to Calculate the Area of Trapezoids?
• How to Find Missing Angels in Quadrilateral Shapes?

Each of these quadrilaterals reviewed above has its characteristics. Although, there are several characteristics common to every quadrilateral. These are:

• They’ve got \(4\) sides.
• They’ve got \(4\) vertices.
• They’ve got \(2\) diagonals.
• The total of all the interior angles equals \(360°\).

We’ll study the additional characteristics of various quadrilaterals closely. We can identify quadrilaterals by utilizing the subsequent characteristics of quadrilaterals.

Squares

Squares are quadrilaterals having \(4\) identical sides as well as \(4\) right angles.

Squares have:

• \(4\) identical sides
• \(4\) right angles
• \(2\) pairs of parallel sides
• \(2\) identical diagonals
• Diagonals that are perpendicular to one another
• Diagonal which bisect one another.

Rectangles

Rectangles are quadrilaterals having \(2\) pairs of identical and parallel opposite sides as well as \(4\) right angles.

Rectangles have:

• \(2\) pairs of parallel sides
• \(4\) right angles
• Opposite sides of identical lengths
• \(2\) identical diagonals
• Diagonals that bisect one another

Parallelograms

Parallelograms are quadrilaterals where both pairs of opposite sides are parallel.

Parallelograms have:

• \(2\) pairs of parallel sides
• Opposing sides of identical lengths
• Opposing angles which are identical
• \(2\) diagonals that bisect one another.

Trapeziums

Trapeziums are quadrilaterals where \(1\) pair of opposing sides are parallel.

• The sides parallel to one another are known as bases.
  In the figure above, GH and EF are bases.
• The sides that are not parallel to one another are known as legs.
  In the figure above, FH and are legs.

Quadrilaterals and Rectangles – Example 1:

Write the appropriate name of each quadrilateral.

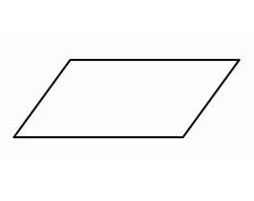
Solution:

In this shape, both pairs of opposite sides are parallel. So, this quadrilateral is a parallelogram.

Quadrilaterals and Rectangles – Example 2:

What is the perimeter of a rectangle whose length is \(14\) cm and whose width is \(9\) cm?

Solution:

The formula for the perimeter of a rectangle = \(2\) (Length + Width). So, the perimeter of a rectangle \(= 2(14+9)=46\)

Exercises for Quadrilaterals and Rectangles

1. Write the appropriate name of each quadrilateral.

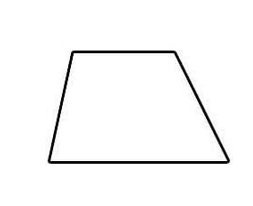
2. What is the perimeter of a rectangle whose length is \(20\) cm and whose width is \(15\) cm?

1. \(\color{blue}{Trapezoid}\)
2. \(\color{blue}{70}\)