In this article, you will learn how to find missing angles in Quadrilateral shapes.
Step by step guide to Find Quadrilateral angles
The following diagram shows a quadrilateral \(ABCD\) and the sum of its internal angles. A perfect quadrilateral is a surface obtained from the intersection of four lines and their extension. The sum of the internal angles of each triangle is \(180\) degrees, and since each quadrilateral is made up of two triangles, the sum of the internal angles of each quadrilateral is \(360\) degrees. Thus, \({\angle}A+{\angle}B+{\angle}C+{\angle}D=360^{\circ}\).
A rectangle is a type of quadrilateral in which both adjacent sides are perpendicular to each other and form right angles. all a rectangle’s angles are \(90^{\circ}\). \({\angle}A+{\angle}B+{\angle}C+{\angle}D=360^{\circ}\).
A square is a quadrilateral, in other words, it is a geometric shape that has four sides, all of which are equal to each other and form a \(90-\)degree or right angle with each other. \({\angle}A+{\angle}B+{\angle}C+{\angle}D=360^{\circ}\).
The parallelogram is a simple quadrilateral with two pairs of parallel sides. The size of the opposite sides and the opposite angles in the parallelogram are equal. \({\angle}A+{\angle}B+{\angle}C+{\angle}D=360^{\circ}\).
Finding Quadrilateral angles Example 1:
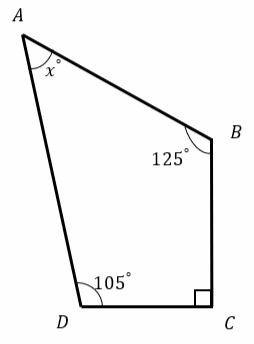
Find the missing angle in the quadrilateral.
Solution: We have been given three angles and need to determine the measure of the fourth. Add together the measures of the known angles.
\(125^{\circ}+90^{\circ}+105^{\circ}=320^{\circ}\)
Subtract the sum from \(360^{\circ}\) to determine what remains for the fourth angle. \(360^{\circ}-320^{\circ}=40^{\circ}\)
The measure of the unknown angle is \(40^{\circ}\)
Finding Quadrilateral angles Example 2:
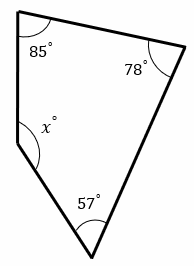
Find the missing angle in the quadrilateral.
Solution: We have been given three angles and need to determine the measure of the fourth. Add together the measures of the known angles.
\(78^{\circ}+85^{\circ}+57^{\circ}=220^{\circ}\)
Subtract the sum from \(360^{\circ}\) to determine what remains for the fourth angle. \(360^{\circ}-220^{\circ}=140^{\circ}\)
The measure of the unknown angle is \(140^{\circ}\)
Exercises for Finding Quadrilateral angles
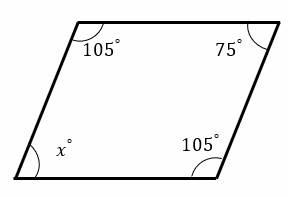
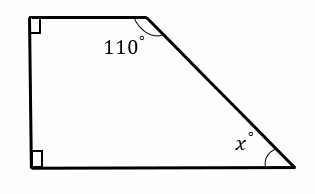
Find the missing angle in each quadrilateral.
1)\(x=\)
2)\(x=\)
3)\(x=\)
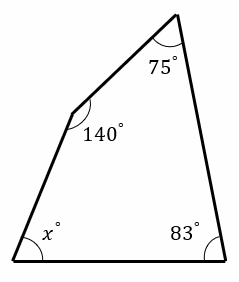
- \(x=75^{\circ}\)
- \(x=70^{\circ}\)
- \(x=62^{\circ}\)
