How to Graph Box Plot?
TL;DR: Want to summarize a whole data set in one quick picture? A box plot does it with just five numbers: minimum, Q1, median, Q3, and maximum. The box itself stretches from Q1 to Q3 with a line at the median, giving you the middle 50 percent of your data at a glance. Whiskers reach out to the smallest and largest non-outlier values, and any true outliers float off as separate dots. Read one and you instantly know the spread, the center, and the weird points.
Key takeaways:
- Box plots show the five-number summary: min, Q1, median, Q3, max.
- The box spans Q1 to Q3, so its width is the IQR.
- A line inside the box marks the median (Q2), splitting the data in half.
- Whiskers extend to the smallest and largest values within \(1.5\,\text{IQR}\) of the box.
- Points outside the whiskers (the \(1.5\,\text{IQR}\) fences) are plotted as outliers.
A box diagram is a special type of diagram that shows the quartiles in a box and the line that extends from the lowest to the highest value.
Related Topics
A step-by-step guide to the box plot
A method for summarizing a set of data that is measured using an interval scale is called a box-and-whisker plot. These are mostly used for data analysis. We use these types of charts or graphs to know:
- Distribution shape
- A central value of it
- Variability of it
A box plot is a graph that shows data from a five-number summary containing one of the measures of central tendency. It does not show the distribution in particular as much as a stem and leaf plot or a histogram does. But it is primarily used to indicate whether a distribution is skewed or not, and if there are potential unusual observations (also called outliers) present in the data set.
Parts of box plots
- Minimum: The minimum value in the given dataset.
- First Quartile \((Q1)\): The first quarter is the middle of the lower half of the data set.
- Median: The median is the middle value of the dataset that divides the given dataset into two equal parts. The median is considered the second quartile.
- Third Quartile \((Q3)\): The third quartile is the middle of the upper half of the data.
- Maximum: The maximum value in the given dataset.
Apart from these five terms, the other terms used in the box diagram are:
- Interquartile Range \((IQR)\): The difference between the third quartile and first quartile is known as the interquartile range. \(IQR = Q3-Q1\)
- Outlier: The data that falls on the far left or right side of the sorted data is tested to be the outlier. In general, the outliers fall more than the specified distance from the first and third quartiles. Outliers are greater than \(Q3+(1.5\times IQR)\) or less than \(Q1-(1.5\times IQR)\).
Box plot distribution
The box diagram distribution explains how the data is grouped, how the data is skewed, and also the symmetry of the data.
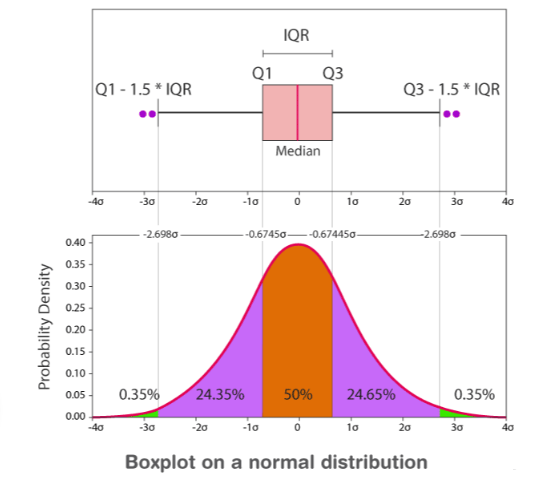
- Positively Skewed: If the distance from the middle to the maximum is greater than the distance from the middle to the minimum, the box diagram has a positive skew.
- Negatively Skewed: If the distance from the middle to the minimum is greater than the distance from the middle to the maximum, the box diagram will be negatively skewed.
- Symmetric: If the median is equidistant from the maximum and minimum values, the box plot is symmetric.
Box plot chart
In a box and whisker plot:
- The end of the box is the top and bottom quadrants so that the box crosses the interquartile range.
- A vertical line inside the box marks the median.
- The two lines outside the box are the whiskers drawn to the highest and lowest observations.
Box Plot – Example 1:
Find the maximum, minimum, median, first quartile, and third quartile for the given data set: \(24, 46, 12, 10, 15, 14, 8\).
Solution:
Given: \(24, 46, 12, 10, 15, 14, 8\).
Arrange the given dataset in ascending order.
\(8, 10, 12, 14, 15, 24, 46\)
Therefore,
Minimum \(= 8\)
Maximum \(= 46\)
Median \(= 14\)
First quartile \(= 10 \left(Middle\:value\:of\:\:8,\:10,\:12\:is\:10\right)\:\)
Third quartile \(= 24 \left(Middle\:value\:of\:15,\:24,\:46\:is\:24\right)\).
Exercises for Box Plot
Draw a box and whisker plot for each data set.
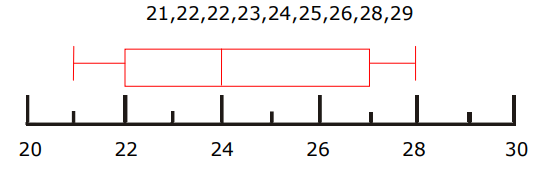
- \(\color{blue}{22, 24, 25, 26, 21, 22, 28, 29, 23}\)
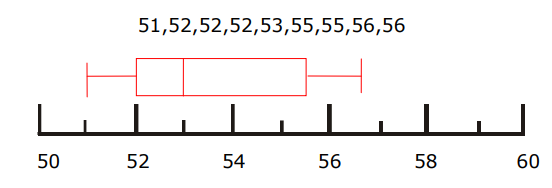
- \(\color{blue}{51, 53, 52, 56, 52, 55, 55, 56, 52}\)
Recommended EffortlessMath Books
For a full Algebra II treatment that includes the statistics and probability you’ll see on tests, Algebra II for Beginners walks through every topic step by step with worked examples. To go deeper into stats specifically, Statistics for Beginners covers descriptive and inferential statistics with practice sets.
Frequently Asked Questions
What is a box plot?
A box plot (also called a box-and-whisker plot) is a compact display of a data set’s five-number summary: minimum, first quartile (Q1), median, third quartile (Q3), and maximum. The box shows the middle 50% of the data, the median line splits the data in half, and whiskers stretch to the smallest and largest non-outlier values. It’s perfect for comparing distributions side by side.
What’s the five-number summary?
The five-number summary lists five values that capture the shape and spread of a data set: minimum, Q1, median, Q3, and maximum. Together they describe both center (median) and spread (IQR, full range). For the data set \(\{2, 5, 7, 8, 10, 12, 14, 17, 19, 22\}\), the summary is \(2, 7, 11, 17, 22\).
How do you find Q1 and Q3 by hand?
Sort the data and find the median (Q2). Q1 is the median of the lower half (all values below the overall median); Q3 is the median of the upper half. For 10 sorted values \(\{2, 5, 7, 8, 10, 12, 14, 17, 19, 22\}\), the lower half is \(\{2, 5, 7, 8, 10\}\) with median 7, so \(Q_1 = 7\). The upper half is \(\{12, 14, 17, 19, 22\}\) with median 17, so \(Q_3 = 17\).
What does the width of the box show?
The width of the box equals the interquartile range, \(\text{IQR} = Q_3 – Q_1\). A wide box means the middle 50% of values is spread out; a narrow box means they’re tightly packed. Comparing two box plots side by side, the wider box has more variability in its middle half.
How long are the whiskers?
Whiskers stretch from each side of the box to the most extreme data value that is still within \(1.5\,\text{IQR}\) of the box edge. Anything beyond those fences is plotted as a separate outlier dot. If your data has no outliers, whiskers go from the box to the actual min and max.
How do you spot outliers on a box plot?
Outliers are the lone dots (or asterisks) sitting beyond the whiskers. A point is flagged as an outlier when it falls below \(Q_1 – 1.5\,\text{IQR}\) or above \(Q_3 + 1.5\,\text{IQR}\). Always check whether an outlier is a data error or a real but unusual value – both happen.
How can I tell if the data is skewed?
Look at where the median line sits inside the box and how long each whisker is. If the median sits closer to Q1 and the right whisker is longer, the data is right-skewed (positive skew). If the median is closer to Q3 and the left whisker is longer, it’s left-skewed. A roughly centered median with similar-length whiskers signals symmetric data.
How do I compare two data sets with box plots?
Plot both box plots on the same axis. Compare medians (which group has the higher center?), IQRs (which is more spread out?), and overall ranges (where are the extremes?). Side-by-side box plots make group comparisons quick – they’re a favorite of AP Statistics free-response questions for that reason.
Box plot vs. histogram – when do I use which?
Histograms show the full shape of the distribution (peaks, gaps, multimodality), so they’re better when you want detail. Box plots compress everything to five numbers, which makes them ideal for comparing several groups at once. Use a histogram for a single data set you want to understand deeply; use box plots for two or more data sets you want to compare quickly.
Where do box plots show up on tests?
State tests grade 6 and up, the SAT, ACT, GRE, AP Statistics, college placement exams, and most stats-related teacher-licensure tests. Common question types: read off the median or IQR from a box plot, identify outliers, compare two distributions, or sketch a box plot from a list of data.
Related EffortlessMath Lessons
If a topic on this page feels rusty, these short lessons go deeper:
Related to This Article
More math articles
- Decoding The Ding Ding Ding: How Math Can Unlock The Secrets Of Slot Machine
- 10 Most Common 4th Grade Georgia Milestones Assessment System Math Questions
- 10 Most Common 5th Grade MCAS Math Questions
- Math learning support for visual learners through browser tools
- Grade 3 Math: Graphs
- Comparing and Ordering Decimals for 5th Grade: Step-by-Step Guide
- 49 Free AASA Grade 3 Math Worksheets for Arizona Students (One Skill Per Page)
- How to Prepare for the FSA Math Test?
- Illinois Grade 2 Math Worksheets — Free Printable PDFs
- Free Grade 5 English Worksheets for Iowa Students
What people say about "How to Graph Box Plot? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.