How to Divide Polynomials Using Synthetic Division?

In mathematics, there are two different ways to divide polynomials. One is the long division method. Another method is synthetic division. Between the two methods, the shortcut method for dividing polynomials is the synthetic division method.

Related Topics

• The Remainder Theorem

A step-by-step guide to dividing polynomials by using synthetic division

Synthetic division is a method used to perform the division operation on polynomials when the divisor is a linear factor. One of the advantages of using this method over the traditional long method is that the synthetic division allows the person to calculate variables without writing them while doing polynomial division, which also makes it easier than the long method.

Synthetic division of polynomials definition

When we divide a polynomial \(p(x)\) by a linear factor \((x – a)\) (which is a polynomial of degree \(1\)), \(Q(x)\) is the quotient polynomial and \(R\) is the remainder.

\(\color{blue}{\frac{p(x)}{q(x)} = \frac{p(x)}{(x- a)} = Quotient + (\frac{Remainder}{(x – a)})}\)

\(\color{blue}{\frac{p(x)}{(x – a)} = Q(x) + (\frac{R}{(x – a)})}\)

We use synthetic division to evaluate polynomials by the remainder theorem, wherein we evaluate the value of \(p(x)\) at \(a\) while dividing \((\frac{p(x)}{(x – a)})\). That is, to find if \(a\) is the factor of the polynomial \(p(x)\), use the synthetic division to find the remainder quickly.

Synthetic division method

The following steps are taken when performing synthetic division and finding the quotient and remainder.

• Check if the polynomial is in the standard form.
• Write the coefficients in the dividend’s place and write the zero of the linear factor in the divisor’s place.
• Bring the first coefficient down.

• Multiply it with the divisor and write it below the next coefficient.
• Add them and write the value below.

• Repeat the previous \(2\) steps until you reach the last term.

• Separate the last term thus obtained which is the remainder.
• Now group the coefficients with the variables to get the quotient.

Note that the resultant polynomial is of one order less than the dividend polynomial.

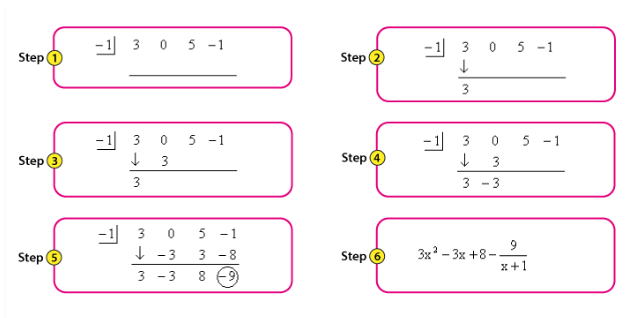
Dividing Polynomials by Using Synthetic Division – Example 1:

Solve by using the synthetic division method. \(\frac{3x^3+5x-1}{x+1}\)

Exercises for Dividing Polynomials by Using Synthetic Division

Perform synthetic division to find the quotient of the following expression.

1. \(\color{blue}{\frac{4x^3-8x^2-x+5}{2x-1}}\)
2. \(\color{blue}{\frac{x^3-5x^2+3x+7}{x-3}}\)
3. \(\color{blue}{\frac{8x^3+12x^2-2x}{4x^2-1}}\)

1. \(\color{blue}{2x^2-3x-2+\frac{3}{2x-1}}\)
2. \(\color{blue}{x^2-2x-3-\frac{2}{x-3}}\)
3. \(\color{blue}{2x+3+\frac{3}{4x^2-1}}\)