How to Find Angles of Quadrilateral Shapes?

A quadrilateral has \(4\) angles. If we know the \(3\) angles of a quadrilateral, we can find the \(4th\) angle of a quadrilateral

A step-by-step guide to finding angles of quadrilateral shapes

There are four interior angles in a quadrilateral that add up to \(360\) degrees. This value is obtained using the sum of the angles of a quadrilateral.

According to the angle sum property of a polygon, the sum of the interior angles of a polygon can be calculated by the number of triangles formed in it. These triangles are formed by drawing diagonals from a single vertex. To make it easier, it can be calculated with a formula that says that if a polygon has \(n\) sides, there will be a triangle \((n – 2)\) inside it.

The sum of the interior angles of a polygon can be calculated by the following formula:

\(S = (n-2) × 180°\),

where \(n\) represents the number of sides of a given polygon.

Interior and exterior angles of the quadrilateral

There are \(4\) interior and \(4\) exterior angles in a quadrilateral. To understand the difference between the interior and exterior angles of a quadrilateral, consider the following figure.

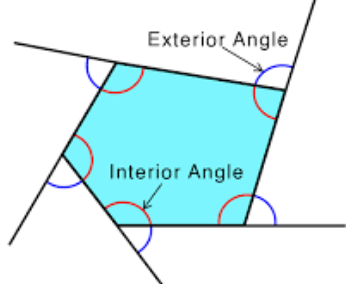
Interior angles of a quadrilateral

The angles inside a quadrilateral are called interior angles. The sum of the interior angles of a quadrilateral is \(360°\). This helps to calculate the unknown angles of a quadrilateral. If a quadrilateral is square or rectangular, we know that all its interior angles are \(90°\) each.

Exterior angles of a quadrilateral

The angles that form between one side of a quadrilateral and another line that extends from an adjacent side are called the exterior angles.

If we look at the figure above, we see that the exterior angle and the interior angle form a straight line, and hence, they make a linear pair.

Therefore, if the interior angle of a quadrilateral is known, we can find the value of the corresponding exterior angle. If the quadrilateral is square or rectangular, all its exterior angles will be \(90°\) each.

Angles of quadrilateral formula

There are some basic formulas for the interior and exterior angles of a quadrilateral:

1. \(\color{blue}{Exterior\:angle\:=\:180°\:-\:Interior\:angle}\). This formula is used when the interior angle of a quadrilateral is known and the corresponding exterior angle value is required. Since both of them form a linear pair, they are supplementary, meaning that their sum is always equal to \(180°\). This formula can also be used to find the interior angle if the corresponding exterior angle is given. In that case, the formula would be \(\color{blue}{Interior\:angle\:=\:180°\:-\:Exterior\:angle}\).
2. If \(3\) angles of a quadrilateral are known, the fourth angle can be calculated using the formula: \(\color{blue}{360\:-\:\left(sum\:of \:3\:other\:interior\:angles\right)}\).
3. The sum of interior angles of a quadrilateral \(\color{blue}{=\:Sum=\left(n\:−\:2\right)\:×\:180°}\), where \(n\) represents the number of sides of the given polygon. 

Finding Angles of Quadrilateral Shapes – Example 1:

If \(3\) interior angles of a quadrilateral are given as \(76°, 99°\), and \(112°\), find the \(4th\) angle.

Solution: 

The \(4th\) angle of the quadrilateral can be calculated using the formula: \(360\:-\:\left(Sum\:of\:the\:other\:3\:interior\:angles\right)\)

Unknown \(4th\) angle \(= 360\:-\:\left(76°\:+\:99°+\:112°\right)\)

\(4th\) angle \(= 360\:- 287=\:73°\)

Exercises for Finding Angles of Quadrilateral Shapes

Find the measure of each angle indicated.

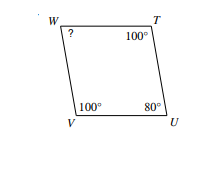
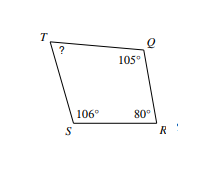
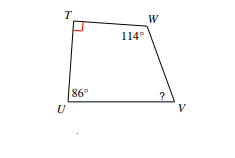
1. \(\color{blue}{80^{\circ }}\)
2. \(\color{blue}{69^{\circ }}\)
3. \(\color{blue}{70^{\circ }}\)