Polygon Names
Want to know more about polygons? We will help you with this in this article.

In geometry, a polygon is a plane figure defined by a finite amount of straight-line segments linked to create a closed polygonal chain (or polygonal circuit).
These segments of a polygonal circuit are termed its sides. The points where \(2\) edges meet up are termed the polygon’s vertices (singular: vertex) or its corners. The inside of a solid polygon is occasionally called the body.
The regular polygon has all of its angles equivalent as well as all of its sides equivalent, if not it’s irregular
Some info on the meaning of a polygon which can with any luck assist you in remembering:
- Flat- Signifies it is a plane figure or \(2\)-dimensional
- Straight lines – Known as segments in geometry
- Enclosed – Every line connects end-to-end and forms a figure without any openings.
Related Topics
- Area and Perimeter
- Perimeters and Areas of Squares
- Perimeters and Areas of rectangles
- How to Find the Perimeter of Polygons?
How is a polygon with N-sides named?
When it comes to its names, polygons have a quite basic name for the first \(10\) or \(20\) names. They utilize a fundamental prefix labeling system. It consists of di, tri, tetra, Penta, etc.
An n-gon is a polygon that has n sides; for instance, a triangle is a \(3\)-gon. In easier terms, a \(24\)-sided polygon. You can usually call it a \(24\)-gon.
Triangle:
Triangles are polygons with \(3\) edges and \(3\) vertices. It’s an example of the fundamental shapes seen in geometry. With Euclidean geometry and \(3\) points, whenever non-collinear, establish a distinctive triangle.
Quadrilateral:
Within geometry, a quadrilateral is a \(4\)-sided polygon, which has \(4\) edges (sides) as well as \(4\) corners (vertices). The name comes from the Latin terms Quadri, a variation of \(4\), and latus, signifying “side.” A different term for it is called tetragon, which comes from the Greek language.
Quadrilaterals are either straightforward (not self-intersecting), or complicated (self-intersecting, or crossed). Straightforward quadrilaterals will be concave or convex.
Inside angles of a straightforward (and planar) quadrilateral, ABCD equal \(360\) degrees of an arc.
Pentagons:
Within geometry, a pentagon (from the Greek representing five and gonia signifying angle) is any \(5\)-sided polygon or a \(5\)-gon. The total of the inner angles in a straightforward pentagon equals \(540°\).
A pentagon can be straightforward or self-intersecting. A self-intersecting regular pentagon (or a star pentagon) is known as a pentagram.
Hexagons:
Within geometry, a hexagon (comes from the Greek hex, which means “six”, along with gonía, which means “corner, angle”) is a \(6\)-sided polygon or a \(6\)-gon. The sum of the inner angles of any straightforward (non-self-intersecting) hexagon equals \(720°\).
Heptagons:
Within geometry, heptagons or septagons are a \(7\)-sided polygon or a \(7\)-gon.
Heptagons are seven-sided shapes, or more precisely, seven-sided polygons. Normal heptagons have \(7\) identical sides as well as \(7\) identical angles.
The amount of the angles of a normal Heptagon equals \(900°\).
Octagons:
Within geometry, octagons are \(8\)-sided polygons or \(8\)-gons. The total of all of their inner angles equals \(1080°\). Like every polygon, the outer angles equal \(360°\).
Nonagons:
Nonagons are polygons having nine sides as well as nine angles. Nonagon = Nona + gon whereas Nona stands for \(9\) and gon stands for sides.
Nonagons have nine angles. The total of angles in a nonagon equals \(1260°\). Nonagons have nine outer angles. The total of the angles of the outer angles for nonagons is \(360°\).
Decagons:
Decagons are polygons with \(10\) sides, \(10\) inner angles as well as \(10\) ten vertices. The total quantity of the inner angles of a straightforward decagon equals \(1440°\).
Polygon Names – Example 1:
Write the name of the figure.
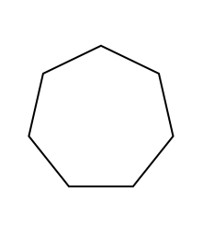
Solution:
This shape is a \(7\)-sided polygon so it is a heptagon.
Polygon Names – Example 2:
Write the name of the figure.

Solution:
This shape is a \(3\)-sided polygon so it is a triangle.
Exercises for Polygon Names
Write the name of the polygons.
1)
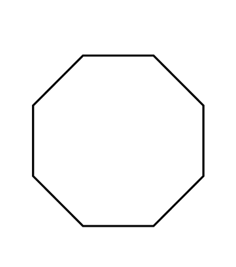
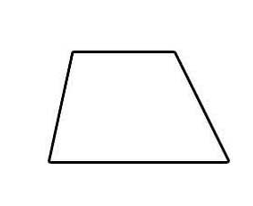
2)

- \(\color{blue}{Octagon}\)
- \(\color{blue}{Quadrilateral}\)
Related to This Article
More math articles
- The Ultimate 6th Grade RICAS Math Course (+FREE Worksheets)
- Comparison and Number Ordering
- ACT Math: Test-Taking Strategies
- How to Identify Characteristics of Quadratic Functions: Equations
- Math Education in the Digital Age: Techniques for Today’s Classroom
- Complete Guide to Mastering Logic and Truth Tables
- Top 10 ISEE Upper-Level Math Practice Questions
- OAR Math Worksheets: FREE & Printable
- How to Find Distance and Midpoint of Complex Numbers?
- Why Math is a Difficult Subject?


























What people say about "Polygon Names - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.