PERT Math FREE Sample Practice Questions
Preparing for the PERT Math test? To succeed on the PERT Math test, you need to practice as many real PERT Math questions as possible. There’s nothing like working on PERT Math sample questions to measure your exam readiness and put you more at ease when taking the PERT Math test. The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your PERT Math test.
Check out our sample PERT Math practice questions to find out what areas you need to practice more before taking the PERT Math test!
Start preparing for the 2026 PERT Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the PERT Math Test
\)
7- Solve.
\(|9 – (12 ÷ | 2 – 5 |)| = \)?
A. 9
B. \(-6\)
C. 5
D. \(-5\)
8- If \(log_{2}x = 5\), then \(x = \)?
A. \(2^{10}\)
B. \(\frac{5}{2}\)
C. \(2^{6}\)
D. 32
9- What’s the reciprocal of \(\frac{x^3}{16}\)?
A. \(\frac{16}{x^3}-1\)
B. \(\frac{48}{x^3}\)
C. \(\frac{16}{x^3}+1\)
D. \(\frac{16}{x^3}\)
10- Find the inverse function for \(ln (2x + 1)\)?
A. \(\frac{1}{2}(e^{x }– 1)\)
B. \((e^{x }+ 1)\)
C. \(\frac{1}{2}(e^{x }+ 1)\)
D. \((e^{x }– 1)\)
Best PERT Math Prep Resource for 2026
Answers:
1- C
METHOD ONE
\(log_4(x+2) – log_4(x-2) = 1\)
Add \(log_4(x-2)\) to both sides
\(log_4(x+2) – log_4(x-2)+ log_4(x-2)= 1 + log_4(x-2)\)
\(log_4(x+2) = 1 + log_4(x-2)\)
Apply logarithm rule:
\(a = log_b(b^a) ⇒ 1 = log_4(4^1) = log_4(4)\)
then: \(log_4(x+2) = log_4(4) + log_4(x-2)\)
Logarithm rule: \(log_c(a) + log_c(b) = log_c(ab)\)
then: \(log_4(4) + log_4(x-2) = log_4(4(x-2))\)
\(log_4(x+2) = log_4(4(x-2))\)
When the logs have the same base:
\(log_b(f(x)) = log_b(g(x)) ⇒ f(x) = g(x)
(x+2) = 4(x-2)\)
\(x = \frac{10}{3}\)
METHOD TWO
We know that:
\(log_ab-log_ac=log_a\frac{b}{c}\space and \space log_ab=c⇒b=a^c\)
Then: \(log_4(x+2)- log_4(x-2)=log_4\frac{(x + 2)}{(x – 2)}=1⇒\frac{(x + 2)}{(x – 2)}=4^1=4⇒x+2=4(x-2)
⇒x+2=4x-8⇒4x-x=8+2→3x=10⇒x=\frac{10}{3}\)
2- B
\(e^{(5x + 1 )}= 10\)
If \( f(x) = g(x)\), then \(ln(f(x)) = ln(g(x))\)
\(ln(e^{(5x + 1 )})= ln(10)\)
Apply logarithm rule:
\(log_a(x^b) = b log_a(x)\)
\(ln(e^{(5x + 1 )})= (5x + 1)ln(e)\)
\((5x + 1)ln(e) = ln(10)\)
\((5x + 1)ln(e) = (5x + 1)\)
\((5x + 1) = ln(10) \)
\( ⇒x = \frac{ln(10) – 1}{5}\) For education statistics and research, visit the National Center for Education Statistics.
3- C
\(f(x) = x –\frac{5}{3}⇒ y = x – \frac{5}{3}⇒ y+ \frac{5}{3}=x\)
\(f^{-1 }= x+ \frac{5}{3}\)
\(f ^{–1}(5) = 5 +\frac{5}{3}=\frac{20}{3}\) For education statistics and research, visit the National Center for Education Statistics.
4- C
cos \(30^{\circ} = \frac{\sqrt 3}{2}\) For education statistics and research, visit the National Center for Education Statistics.
5- C
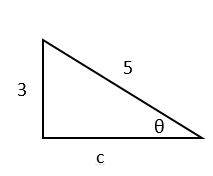
sin\(θ=\frac{3}{5}⇒\) we have following triangle, then:
\(c=\sqrt {(5^2-3^2 )}=\sqrt{(25-9)}=\sqrt 16=4\)
cos\(θ=\frac{4}{5}\) For education statistics and research, visit the National Center for Education Statistics.
6- B
\(-2x- y = -9\)
\(5x-2y= 18\)
\(⇒\) Multiplication \((–2)\) in first equation
\(4x +2y =18\)
\(5x-2y= 18\)
Add two equations together \(⇒ 9x =36 ⇒ x= 4\) then: \(y = 1\) For education statistics and research, visit the National Center for Education Statistics.
7- C
\(|9 – (12 ÷ | 2 – 5 |)| = |(9-(12÷|-3|))|=|9-(12÷3)|=|9-4|=|5|=5\)
8- D
METHOD ONE
\(log_{2}x = 5\)
Apply logarithm rule: \(a = log_b(b^a)\)
\(5 = log_2(2^5) = log_2(32)\)
\(log_2x = log_2(32)\)
When the logs have the same base: \(log_b(f(x)) = log_b(g(x))⇒ f(x) = g(x)\)
then: \(x = 32\)
METHOD TWO
We know that:
\(log_ab=c⇒b=a^c \)
\(log_2x=5⇒x=2^5=32\)
9- D
\(\frac{x^3}{16}\)
\(⇒\) reciprocal is : \(\frac{16}{x^3}\)
10- A
\(f(x) = ln (2x + 1)\)
\(y = ln (2x + 1)\)
Change variables \(x\) and \(y: x = ln (2y + 1)\)
solve: \(x = ln (2y + 1)\)
\(y = \frac{e^{x}-1}{2}=\frac{1}{2}(e^{x} – 1)\)
The Best Book to Ace the PERT Test
More from Effortless Math for PERT Test …
Looking for a PERT math study guide to help you prepare for your PERT Math test?
Top 5 PERT Math Study Guides will introduce you to the books for the PERT Math test!
Do you want to get your desired result in the PERT math test?
Do not forget to follow the important tips of the test day!: PERT Math – Test Day Tips.
Can’t handle the difficult math questions on the PERT test?
The best way to handle this is by reviewing the Top 10 PERT Math Practice Questions.
The Perfect Prep Books for the PERT Math Test
Have any questions about the PERT Test?
Write your questions about the PERT or any other topics below and we’ll reply!
Related to This Article
More math articles
- Geometry Puzzle – Challenge 62
- How to Show the Relation in the Coordinate Plane
- How Math Can Help You Win At Poker?
- 8th Grade CMAS Math Worksheets: FREE & Printable
- How to Find Magnitude of Vectors?
- Top 10 SAT Math Practice Questions
- 6th Grade PACE Math Worksheets: FREE & Printable
- 5th Grade OST Math FREE Sample Practice Questions
- How to Solve Multiplication Rule for Probabilities?
- Rules of Exponents
What people say about "PERT Math FREE Sample Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.