How to Calculate the Area of Trapezoids? (+FREE Worksheet!)
Learn more about trapezoids and how to calculate their areas by using the trapezoid area formula.
Related Topics
- How to Find the volume and surface area of Rectangular Prisms
- How to Solve Triangles Problems
- How to Solve Pythagorean Theorem Problems
- How to Find Volume and Surface Area of Cubes
- How to Find the Perimeter of Polygons
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Original price was: $89.99.$49.99Current price is: $49.99.
A step-by-step guide to calculating the area of Trapezoids
- A quadrilateral with at least one pair of parallel sides is a trapezoid.
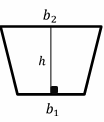
- Area of a trapezoid \(= \color{blue}{\frac{1}{2} h(b_{1}+b_{2})}\)
Area of Trapezoids – Example 1:
Calculate the area of the trapezoid.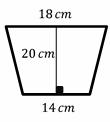
Solution:
Use trapezoid area formula: \(A= \frac{1}{2} h(b_{1}+b_{2 }) \)
\(b_{1}=14 cm , b_{2}=18\) \(cm\) and \(h=20\) \(cm\)
Then: \(A= \frac{1}{2}(20)(14+18)=10(32)=320\) \(cm^2\)
The Best Book to Help You Ace Pre-Algebra
Original price was: $24.99.$14.99Current price is: $14.99.
Satisfied 92 Students
Area of Trapezoids – Example 2:
Calculate the area of the trapezoid.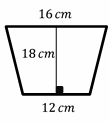
Solution:
Use trapezoid area formula: \(A= \frac{1}{2} h(b_{1}+b_{2 }) \)
\(b_{1}=12 cm , b_{2}=16\) \(cm\) and \(h=18\) \(cm\)
Then: \(A= \frac{1}{2}(18)(12+16)=9(28)=252\) \(cm^2\)
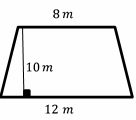
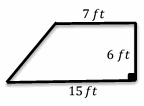
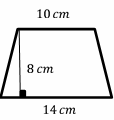
Exercises for Calculating Area of Trapezoids
Calculate the area for each trapezoid.
Download Trapezoids Worksheet
- \(\color{blue}{28 \ cm^2}\)
- \(\color{blue}{100 \ m^2}\)
- \(\color{blue}{66 \ ft^2}\)
- \(\color{blue}{96 \ cm^2}\)
The Greatest Books for Students to Ace the Algebra
Original price was: $29.99.$19.99Current price is: $19.99.
Original price was: $29.99.$19.99Current price is: $19.99.
Original price was: $29.99.$19.99Current price is: $19.99.
Original price was: $29.99.$19.99Current price is: $19.99.
Original price was: $29.99.$17.99Current price is: $17.99.
Related to This Article
More math articles
- How to Multiply and Divide Complex Numbers in Polar Form?
- Other Topics Puzzle – Challenge 98
- Math Courses Required For A Business Degree
- What Are the Applications of the Law of Cosines?
- How to Use Properties of Logarithms? (+FREE Worksheet!)
- How to Solve Logarithmic Equations: Definition and Properties
- How to Master Polynomial Functions: A Comprehensive Guide to Understanding and Solving Complex Zeros
- How to Use the Law of Cosines to Find Angle Measure?
- 4th Grade SBAC Math Worksheets: FREE & Printable
- Number Navigators: How to Select Pairs with Targeted Sums and Differences
What people say about "How to Calculate the Area of Trapezoids? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.