How to Solve Pythagorean Theorem Problems? (+FREE Worksheet!)
In mathematics, the Pythagorean Theorem is the relationship between three sides of a right triangle.
Related Topics
- How Calculate the Area of Trapezoids
- How to Find the volume and surface area of Rectangular Prisms
- How to Solve Triangles Problems
- How to Find Volume and Surface Area of Cubes
- How to Find the Perimeter of Polygons
Step by step guide to solve Pythagorean Theorem problems
- We can use the Pythagorean Theorem to find a missing side in a right triangle.
- In any right triangle: \(\color{blue}{a^2+b^2= c^2}\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
The Pythagorean Theorem – Example 1:
Right triangle ABC has two legs of lengths \(9\) cm (AB) and \(12\) cm (AC). What is the length of the third side (BC)?
Solution:
Use Pythagorean Theorem: \(\color{blue}{a^2+b^2= c^2}\)
Then: \(a^2+b^2= c^2 →9^2+12^2= c^2 →81+144=c^2\)
\(c^2=225 →\) \(c=\sqrt{225}=15\) \(cm\) → \(c=15 cm\)
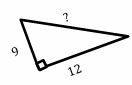
The Pythagorean Theorem – Example 2:
Find the hypotenuse of the following right triangle.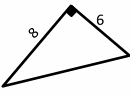 
Solution:
Use Pythagorean Theorem: \(\color{blue}{a^2+b^2= c^2}\)
Then: \(a^2+b^2= c^2 →8^2+6^2= c^2 →64+36=c^2\)
\(c^2=100 →\) \(c=\sqrt{100}=10\) → \(c=10\)
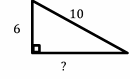
The Pythagorean Theorem – Example 3:
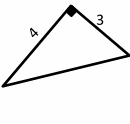
Find the hypotenuse of the following right triangle.
Solution:
Use Pythagorean Theorem: \(\color{blue}{a^2+b^2= c^2}\)
Then: \(a^2+b^2= c^2 →3^2+4^2= c^2 →9+16=c^2\)
\(c^2=25 →\) \(c=\sqrt{25}=5\) → \(c=5\)
The Best Book to Help You Ace Pre-Algebra
The Pythagorean Theorem – Example 4:
Right triangle ABC has two legs of lengths \(6\) cm (AB) and \(8\) cm (AC). What is the length of the third side (BC)?
Solution:
Use Pythagorean Theorem: \(\color{blue}{a^2+b^2= c^2}\)
Then: \(a^2+b^2= c^2 →6^2+8^2= c^2 →36+64=c^2\)
\( c^2=100 →\) \(c=\sqrt{100}=10\) \(cm\) → \(c= 10 cm\)
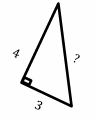
Exercises for Solveing the Pythagorean Theorem
Find the missing side in each right triangle.
Download Pythagorean Relationship Worksheet
- \(\color{blue}{13}\)
- \(\color{blue}{5}\)
- \(\color{blue}{15}\)
- \(\color{blue}{8}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- The Ultimate HiSET Math Course (+FREE Worksheets & Tests)
- Top 10 PSAT 10 Math Practice Questions
- How to Use Number Lines to Graph and Order Fractions
- The Ultimate 7th Grade PSSA Math Course (+FREE Worksheets)
- How to Find the Solutions: “Pre-Algebra for Beginners” Detailed Answer Manual
- How to Use Strip Models to Subtract Fractions with Like Denominators
- How to Identify Graphs of Basic Functions
- How to Calculate Cylinder Volume and Surface Area? (+FREE Worksheet!)
- The Ultimate GACE Elementary Education Math Course
- How Hard Is the ALEKS Math Test?
What people say about "How to Solve Pythagorean Theorem Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.