How to Find the Area and Circumference of Circles? (+FREE Worksheet!)
Learn how how to find the Area and Circumference of Circles when you have the radius or the diameter of the circle.

Related Topics
- How to Find Arc Length and Sector Area
- How to Find Equation of a Circle
- How to Find the Center and the Radius of Circles
The Absolute Best Books to Ace Pre-Algebra to Algebra II
A step-by-step guide to solving Circles
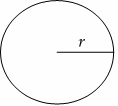
- In a circle, variable \(r\) is usually used for the radius and \(d\) for the diameter, and \(π\) is about \(3.14\).
- Area of a circle \(\color{blue}{=πr^2}\)
- Circumference of a circle \(\color{blue}{=2πr}\)

Circles – Example 1:
Find the area of the circle. 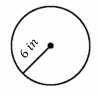
Solution:
Use area formula: Area \(=πr^2\),
\(r=6\) \(in\), then: Area \(=π(6)^2=36π\)
\(π=3.14\), then: Area \(=36×3.14=113.04\) \(in^2\)
Circles – Example 2:
Find the Circumference of the circle. 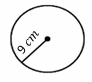
Solution:
Use Circumference formula: Circumference \(=2πr \)
\(r=9 \) \(cm\) , then: Circumference \(=2π(9)=18π \)
\(π=3.14\), then: Circumference \(=18×3.14=56.52\) \(cm\)
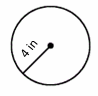
Circles – Example 3:
Find the area of the circle. 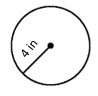
Solution:
Use area formula: Area \(=πr^2\),
\(r=4\) \(in\), then: Area \(=π(4)^2=16π\)
\(π=3.14\), then: Area \(=16×3.14=50.24\) \(in^2\)
Circles – Example 4:
Find the Circumference of the circle. 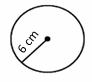
Solution:
Use Circumference formula: Circumference \(=2πr \)
\(r=6 \) \(cm\) , then: Circumference \(=2π(6)=12π \)
\(π=3.14\), then: Circumference \(=12×3.14=37.68\) \(cm\)
The Best Book to Help You Ace Pre-Algebra
Exercises for Solving Circles
Find the area and circumference of each circle. \((\pi=3.14)\)
Download Circles Worksheet

- \(\color{blue}{Area: \ 50.24 \ in^2 , \ Circumference: \ 25.12 \ in}\)
- \(\color{blue}{Area: \ 1,017.36 \ cm^2, \ Circumference: \ 113.04 \ cm}\)
- \(\color{blue}{Area: \ 78.5 \ m^2, \ Circumference: \ 31.4 \ m}\)
- \(\color{blue}{Area: \ 379.94 \ cm^2 , \ Circumference: \ 69.08 \ cm}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- Distance Measurements
- How to Compare Money Amounts
- How to Transform Linear Functions
- FREE 8th Grade PSSA Math Practice Test
- What is the Relationship between Dilations and Angles in Geometry
- Best Online Math Tutoring Devices
- Quadratic Function
- How to Solve the Complex Plane?
- Using Number Lines to Represent Decimals
- How to Graph Proportional Relationships and Find the Slope

















What people say about "How to Find the Area and Circumference of Circles? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.