How to Solve the Complex Plane?
Solve the Complex Plane: what to notice and how to work it
What to notice first
Common student mistake
Key formulas and cues
A reliable path
- Separate partsKeep real and imaginary terms in their own lanes.
- Use i squaredReplace \(i^2\) with -1 whenever it appears.
- Use conjugatesFor division, multiply by the conjugate to make the denominator real.
Worked examples
Add complex numbers
- Add real parts: 4 + 2.
- Add imaginary parts: 3i – 5i.
- Write both parts together.
Use i squared
- Multiply coefficients to get 5.
- i times i is i squared.
- Replace i squared with -1.
Try one before moving on
Solve the Complex Plane: pop-up practice
A complex number has both a real and an imaginary component. It’s the real part that has the number itself. The imaginary part, on the other hand, has the letter \(i\) attached to it. This imaginary \(i\) also has a mathematical definition. Imaginary number rule: \(?^2=−1\)
Related Topics
A step-by-step guide to graph the complex plane
Complex numbers cannot be plotted on a number line in the same way that real numbers can. We can still depict them graphically, though. To represent a complex number, we must consider both of its components.
As a way to represent the real and imaginary components of an object, we utilize a coordinate system known as a “complex plane”.
The complex numbers are positions on the plane represented as ordered pairs \((a, b)\), where \(a\) represents the horizontal axis coordinate and \(b\) represents the vertical axis coordinate.
- How to represent the components of a complex number on the complex plane?
- Calculate the real and imaginary parts of the complex number.
- Show the real component of the number by moving down the horizontal axis.
- To reveal the imaginary component of the number, move parallel to the vertical axis.
- Make a diagram of the spot.
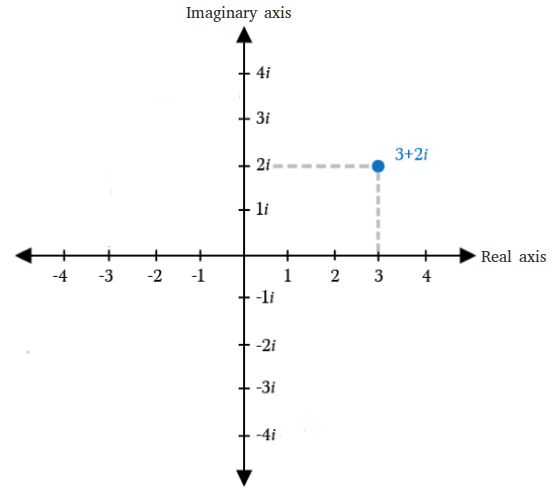
The Complex Plane – Example 1:
Plot the complex number \(3+2i\).
This number has a real part of \(3\) and an imaginary part of \(2\).
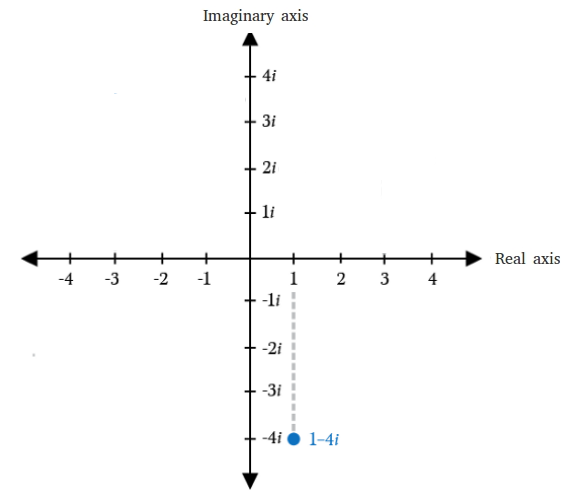
The Complex Plane – Example 2:
Plot the complex number \(1-4i\).
This number has a real part of \(1\) and an imaginary part of \(-4\).
Exercises for the Complex Plane
Graph these complex numbers.
- \(\color{blue}{-3+3.5i}\)
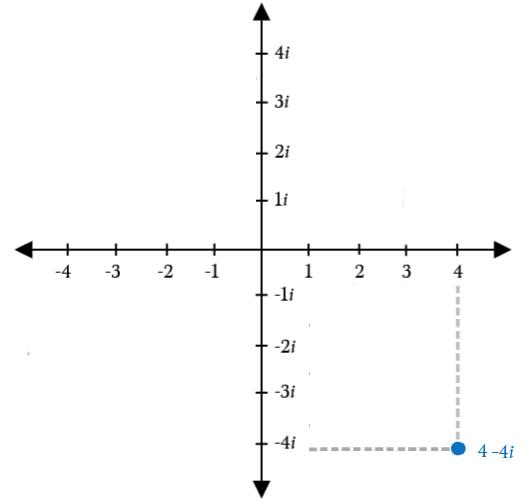
- \(\color{blue}{4-4i}\)
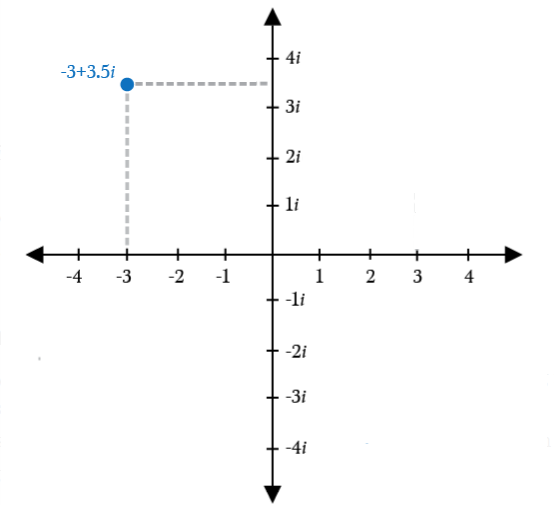
- \(\color{blue}{4-4i}\)
Related to This Article
More math articles
- Best Financial Calculators in the Market
- The Ultimate 6th Grade WY-TOPP Math Course (+FREE Worksheets)
- Full-Length PSAT Math Practice Test-Answers and Explanations
- FREE Praxis Core Math Practice Test
- The Best Grade 8 Math Book for Alabama Students
- How to Find the Central Angle of a Circle?
- A Step into The World of Calculus: Rules of Differentiation
- Writing Functions
- 4th Grade Georgia Milestones Assessment System Math Worksheets: FREE & Printable
- Deciphering Change: Differential Equations in Daily Life
What people say about "How to Solve the Complex Plane? - Effortless Math"?
No one replied yet.