How to Find a Coordinate: Dilation
A Step-by-step Guide to Finding a Coordinate: Dilation
Step 1: Identify the Center of Dilation
Step 2: Determine the Scale Factor
Step 3: Perform the Dilation
Step 4: Plot the Dilated Figure
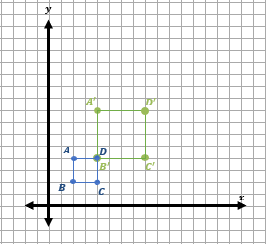
An Example of Coordinate Dilation
Conclusion
Original price was: $109.99.$54.99Current price is: $54.99.
Original price was: $109.99.$54.99Current price is: $54.99.
Original price was: $109.99.$54.99Current price is: $54.99.
Related to This Article
More math articles
- Unlocking the Secrets of Curves: Higher Order Derivatives in Graph Analysis
- 3rd Grade MCAS Math Practice Test Questions
- 4th Grade FSA Math FREE Sample Practice Questions
- The Best Grade 7 ELA Practice Tests for Pennsylvania Students
- Ratio, Proportion and Percentages Puzzle – Challenge 30
- How to Prepare for the Next-Generation ACCUPLACER Math Test?
- How to Unlock the Secrets: “SIFT Math for Beginners” Solution Manual
- How to Solve Quadratic Inequalities? (+FREE Worksheet!)
- Bеѕt Digital Pеn Tablet fоr Onlinе Mаth Teaching in 2026
- Rhode Island Algebra 1 Free Worksheets: Printable Algebra 1 Practice, Fully Worked Keys
What people say about "How to Find a Coordinate: Dilation - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.