How to Graph Translations on the Coordinate Plane?

Step by step guide to Graph Translations on the Coordinate Plane

Translation on the coordinate plane is sliding a point or figure in any direction without any changes in size or shape. In fact, during translation, the coordinates of the vertices of a figure or point change, and they slide left or right, up, or down without changing size or shape.

Translations in a coordinate plane can be described by this coordinate notation: \((x, y)→(x+a, y+b)\), where \(a\) and \(b\) are constants. Each point shifts \(a\) units horizontally and \(b\) units vertically. Note that to graph a translation, you should perform the same change for each point.

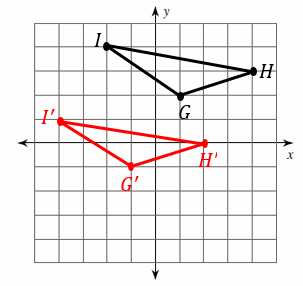
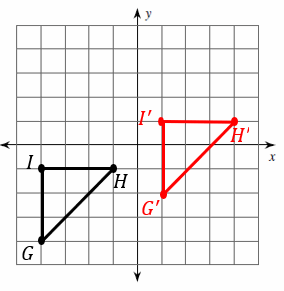
Translations on the Coordinate Plane – Example 1:

Translate triangle IGH \(-2\) units in the \(x-\)direction and \(-3\) units in the \(y-\)direction.

Solution:

First, write the original coordinates of the points:

\(I=(-2, 4)\) \(G=(1, 2)\) \(H=(4, 3)\)

Use this coordinate notation for translating each point: \((x, y)→(x+a, y+b)\)

\(a=-2\), \(b=-3\), then: \((x, y)→(x-2, y-3)\)

Then: \(I^\prime=(-4, 1)\) \(G^\prime=(-1, -1)\) \(H^\prime=(2, 0)\)

Now, find new points on the coordinate plane and graph the new triangle by \(I^\prime, G^\prime, H^\prime\) coordinates.

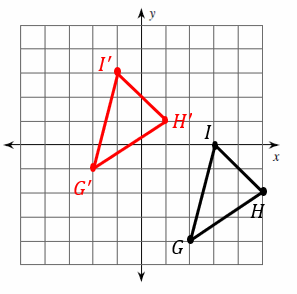
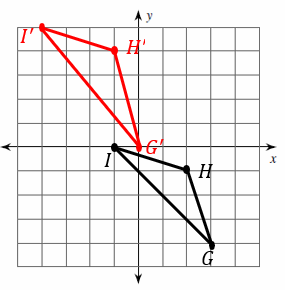
Translations on the Coordinate Plane – Example 2:

Graph the image of the figure using the transformation given.

Translation:  \(4\) units left and \(3\) units up.

Solution:

First, write the original coordinates of the points:

\(I=(3, 0)\) \(G=(2, -4)\) \(H=(5, -2)\)

Use this coordinate notation for translating each point: \((x, y)→(x+a, y+b)\)

\(4\) units left →\(a=-4\)

\(3\) units up →\(b=3\)

Then: \(I^\prime=(-1, 3)\) \(G^\prime=(-2, -1)\) \(H^\prime=(1, 1)\)

Now, find new points on the coordinate plane and graph the new triangle by \(I^\prime, G^\prime, H^\prime\) coordinates.

Exercises for Translations on the Coordinate Plane

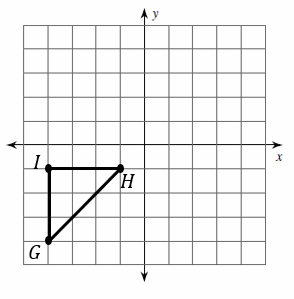
Graph the image of the figure using the transformation given.

1.Translation: \(5\) units right and \(2\) unit up.

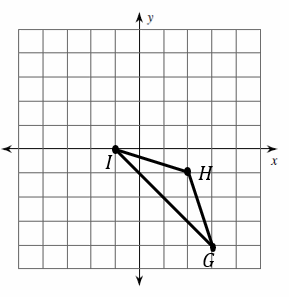
2.Translation: \(3\) units left and \(5\) unit up.