Graph Points on a Coordinate Plane

What’s a Coordinate Plane?

Coordinate planes are two-dimensional surfaces created using \(2\) number lines. It’s created whenever a horizontal line known as the \(X\)-axis as well as a vertical line known as a \(Y\)-axis intersect at a point known as the origin.

The numerals on a coordinate grid get utilized to find points. You can utilize a coordinate plane to graph points, lines, etc. It behaves like a map and produces accurate directions from one place to another.

Related Topics

• Line Graphs
• Bar Graph
• Pie Graphs
• Pictographs and Tally Charts

What are Coordinates?

Coordinates are a collection of \(2\) values that find a precise spot on a coordinate plane grid, more well-known as a coordinate plane.

Points in coordinate planes are named via their ordered pair \((x, y)\), written inside parentheses, equivalent to the \(X\)-coordinate along with the \(Y\)-coordinate.

The coordinates could be positive, negative, or zero, dependent on the position of the point in the respective quadrant.

Quadrants on a Coordinate Plane

Quadrants can be described as an area/part of a cartesian or a coordinate plane achieved whenever the \(2\) axes intersect with each other.

• \(1^{st}\) quadrant: \(x > 0, y > 0\)
• \(2nd\) quadrant: \(x < 0, y > 0\)
• \(3rd\) quadrant: \(x < 0, y < 0\)
• \(4th\) quadrant: \(x > 0, y < 0\)

Finding a Point on a Coordinate Plane

Since we’re already acquainted with coordinate planes and their parts, now we can talk about the way to identify points on a coordinate plane. To find a point on a coordinate plane, follow the steps presented below:

• Step one: Find a point.
• Step two: Find a quadrant by looking at the signs of its \(X\) and \(Y\) coordinates.
• Step three: Find its \(X\)-coordinate or abscissa of the point via reading the number of units the point is to the right/left of the origin along its \(X\)-axis.
• Step four: Find its \(Y\)-coordinate or the ordinate of the point via reading the number of units the point is below/above the origin along its \(Y\)-axis.

Crucial Points on a Coordinate Plane:

• The \(1\)^st quadrant \((+, +)\) called the positive coordinates quadrant is symbolized by the Roman numeral \(I\).
• The \(2\)nd quadrant \((-, +)\) is characterized by the Roman numeral \(II\).
• The \(3\)rd quadrant \((-, -)\) is characterized by the Roman numeral \(III\).
• The \(4\)th quadrant \((+, -)\) is characterized by the Roman numeral \(IV\).
• The coordinates of any point get put into brackets.

Graph Points on a Coordinate Plane – Example:

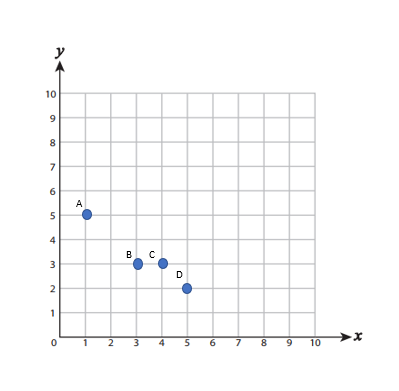
Plot each point on the coordinate grid.

\(A (1,5)\), \(B (3,3)\), \(C(4,3)\), \(D (5,2)\)

Solution:

First, we draw a coordinate axis so that the horizontal axis is the \(x\)-axis and the vertical axis is the \(y\)-axis. Each point with coordinates \((x, y)\) is defined on the axis so that \(x\) denotes the number of units the point is to the right/left of the origin along its \(x\)-axis and \(y\) denotes the number of units the point is below/above the origin along its \(y\)-axis. For example, to specify a point \((1, 5)\) from the origin of the coordinates, we must move one unit to the right and five units to the top.

Exercises for Graph Points on a Coordinate Plane

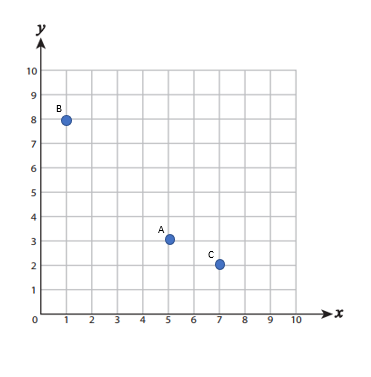
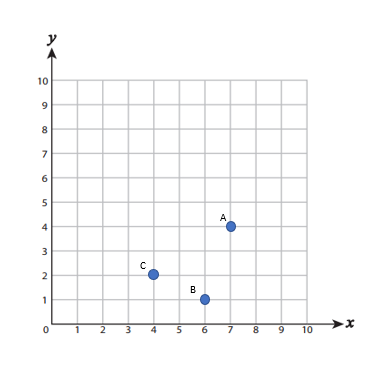
Plot each point on the coordinate grid.

1. \(\color{blue}{A(5,3), B(1,8), C(7,2)}\)
2. \(\color{blue}{A(7,4), B(6,1), C(4,2)}\)

1)

2)