How to Solve Systems of Equations Graphically?

To solve a system of linear equations graphically, we draw both equations in the same coordinate system. The system solution will be at the point where the two lines intersect.

Related Topics

• How to Solve Systems of Equations
• How to Solve Systems of Equations with Substitution

A step-by-step guide to solving systems of equations graphically

Linear equations are algebraic equations in which each sentence has a real constant and the equation consists of \(2\) variables with the highest power of \(1\). The linear equation is represented by \(y=mx + b\), also known as the \(y\)-intercept. Showing a linear equation on a graph is called graphing a linear equation, which is represented as a straight line with one or two variables.

Graphing linear equations

Graphing a linear equation is about solving the linear equations and showing the solution in a coordinate plane. When drawing an equation on a graph, two pairs \((x, y)\) are sufficient. However, we can not know whether there are any mistakes in obtaining these values because the two points can always be joined and represented as a line. Hence, it is recommended to draw another point to ensure the solutions obtained for the given linear equation are correct.

To draw a linear equation with one variable, the following steps must be performed:

• Make sure the linear equation is in \(y\)-intercept form, which is \(y= mx+b\).
• Apply the trial and error method and find the value \((x, y)\) up to three pairs that satisfy the linear equation.
• Find the \(x\)-intercept and \(y\)-intercept of the equation. For \(y\)-intercept, substitute the value of \(x= 0\) in the equation. This results in \(x= a\), for \(x\)-intercept, substitute the value of \(y = 0\) in the equation. This results in \(y= c\).
• Therefore, the points are \((a, 0)\) and \((0, c)\). Make a tabular form and put the value of \(x\) and \(y\) respectively.
• Plot all the points on the graph paper.
• Combine all the points which are marked on the graph and you will get a straight line representing the given linear equation graphically.

Graphing linear equations in two variables

The graph of linear equations in two variables is done in a similar way to one variable. The lines drawn on the diagram can intersect at one point or be parallel to each other, resulting in no solution.

Sometimes, the lines might coincide with each other leaving each point on that line as a solution resulting in the given system having an infinite number of solutions. If the system has a solution, then it is said to be consistent; otherwise, it is said to be inconsistent.

The following steps are used to plot linear equations in two variables:

• To plot a linear equation with two variables, we draw both equations.
• To graph an equation manually, first convert it to the form \(y=mx+b\) by solving the equation for \(y\).
• Start putting the values of \(x\) as \(0, 1, 2\), and so on, and find the corresponding values of \(y\), or vice-versa.
• Identify the point where both lines meet.
• The point of intersection is the solution.

Exercises for Solving Systems of Equations Graphically

Solve each system by graphing.

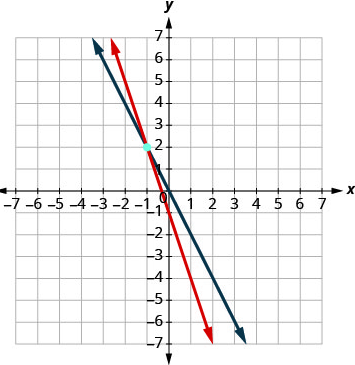
• \(\color{blue}{\begin{cases}3x+y=-1\\ 2x+y=0\end{cases}}\)

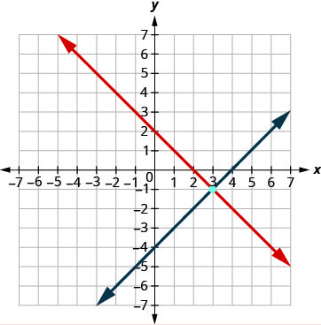
• \(\color{blue}{\begin{cases}x+y=2\\ x-y=4\end{cases}}\)

• \(\color{blue}{\begin{cases}3x+y=-1\\ 2x+y=0\end{cases}}\)

• \(\color{blue}{\begin{cases}x+y=2\\ x-y=4\end{cases}}\)