Intelligent Math Puzzle – Challenge 88
A great mathematical and logic puzzle designed for those interested in school-level Maths. The answer is also given.
[include_netrun_products_block from-products="product/ssat-middle-level-math-for-beginners/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{{url}}/?ajax-add-to-cart={{id}}" product-item-button-custom-url-if-not-salable="{{productUrl}} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
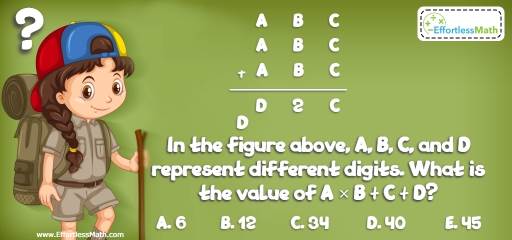
Challenge:
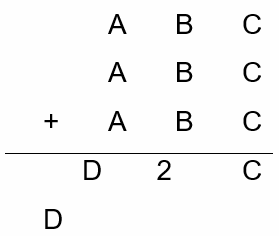
In the figure above, A, B, C, and D represent different digits. What is the value of A × B + C + D?
A- 6
B- 12
C- 34
D- 40
E- 45
The Absolute Best Book to Challenge Your Smart Student!
The correct answer is A.
A, B, C, and D represent different digits. The sum of three 3-digit numbers is a 4-digit number with 1 or 2 in the thousands place. Therefore, D = 1 or 2. And A is 3 or greater than 3. Why?
A + A + A = 12 or 12+1, Why?
Since, A is a digit, then 3A cannot be 13. 3A = 12 ⇒ A = 4
We also know that C + C + C = C or C + 10
C = 0 or 3C = C + 10 → 2C = 10 → C = 5
Therefore, C is 0 or 5.
Let’s assume D = 1. Then:
If C = 0 → B + B + B = 1 or B + B + B = 1 + 10
3B = 1 (This is not correct) or 3B = 1 + 10 (This is not correct either).
If C = 5 → B + B + B + 1 = D → D = 1 → 3B = 1 – 1= 0
or
B + B + B + 1 = D + 10 → 3B + 1 = 1 + 10 → B \(= \frac{10}{3}\)
B is an integer and cannot be \(\frac{10}{3}\).
In this situation, the only value of B is 0.
If A = 4, B = 0 and C = 5, then 405 + 405 + 405 = 1215 Bingo!
You can check out other values for A, B, C, and D. But, only the above values work.
A × B + C + D = 4 × 0 + 5 + 1 = 6
The Best Books to Ace Algebra
Related to This Article
More math articles
- Mastering the Art of Teaching Pre-Algebra with “Pre-Algebra for Beginners”
- How to Determine if (X, Y) is a Solution to a System of Equations
- A Deep Dive Into The World of Trigonometric Limits
- Remainder Riddles: How to Decipher Division with One-digit Divisors
- Unlocking the Secrets of Inscribed Polygons
- A Mathematical Look at Random Number Generators in Games
- TSI Math Formulas
- Trigonometric Ratios
- 10 Most Common 4th Grade MEAP Math Questions
- The Best THEA Math Worksheets: FREE & Printable
What people say about "Intelligent Math Puzzle – Challenge 88 - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.