FREE 6th Grade MCAS Math Practice Test

We know that the time of your student to prepare for the 6th Grade MCAS Math exam is limited! So, in this article, we have decided to select 20 real 6th Grade MCAS Math questions from the past exams for your student so that the student is fully prepared for the 6th Grade MCAS Math exam. Using these questions will increase your student’s chances of getting a high score on the 6th Grade MCAS Math test.

Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions students need to practice.

The Absolute Best Book to Ace the MCAS Math Test

10 Sample 6th Grade MCAS Math Practice Questions

1- There are 55 blue marbles and 143 red marbles. We want to place these marbles in some boxes so that there is the same number of red marbles in each box and the same number of blue marbles in each of the boxes. How many boxes do we need?

A. 8

B. 9

C. 10

D. 11

2- What is the value of the following expression?
\(2,205÷315\)

A. 5

B. 6

C. 7

D. 8

3- Solve the following equation.
\(112=22+x\)

A. \( x=-90\)

B. \( x=90\)

C. \( x=-134\)

D. \( x=134\)

4- Car A travels 221.5 km at a given time, while car B travels 1.2 times the distance car A travels at the same time. What is the distance car B travels during that time?

A. 222.7 km

B. 233.5 km

C. 241.5 km

D. 265.8 km

5- The perimeter of the trapezoid below is 38. What is its area?

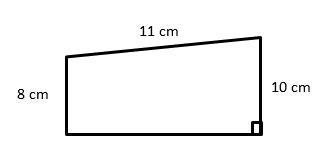
A. 198 cm\(^2\)

B. 162 cm\(^2\)

C. 99 cm\(^2\)

D. 81cm\(^2\)

6- Which of the following expressions has the greatest value?

A. \( 3^1+12\)

B. \( 3^3-3^2\)

C. \( 3^4-60\)

D. \( 3^5-218\)

7- Alfred has \(x\) apples. Alvin has 40 apples, which is 15 apples less than a number of apples Alfred owns. If Baron has \(\frac{1}{5}\) times as many apples as Alfred has. How many apples does Baron have?

A. 5

B. 11

C. 55

D. 275

8- In the following triangle find \(α\).

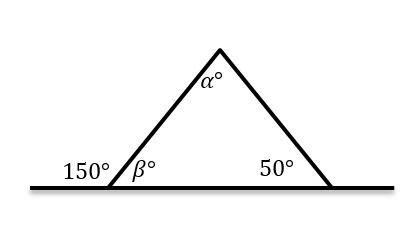
A. \(100^\circ\)

B. \(90^\circ\)

C. \(60^\circ\)

D. \(30^\circ\)

9- The price of a laptop is decreased by \(15\%\) to $425. What is its original price?

A. $283

B. $430

C. $500

D. $550

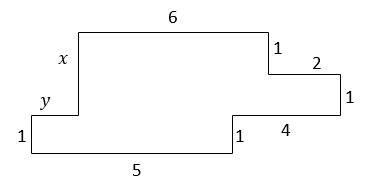
10- Find the perimeter of shape in the following figure? (all angles are right angles)

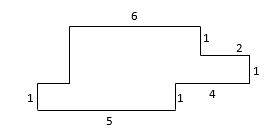
A. 21

B. 22

C. 24

D. 20

11- What are the values of mode and median in the following set of numbers?
\(1,3,3,6,6,5,4,3,1,1,2\)

A. Mode: 1, 2, Median: 2

B. Mode: 1, 3, Median: 3

C. Mode: 2, 3, Median: 2

D. Mode: 1, 3, Median: 2.5

12- Which expression equivalent to \(x × 92\)?

A. \((x×90)+2\)

B. \(x×9×2\)

C. \((x×90)+(x×2)\)

D. \((x×90)+2\)

13- The ratio of pens to pencils in a box is 3 to 5. If there are 96 pens and pencils in the box altogether, how many more pens should be put in the box to make the ratio of pens to pencils 1 : 1?

A. 22

B. 23

C. 24

D. 25

14- If point A placed at \(-\frac{24}{3}\) on a number line, which of the following points has a distance equal to 5 from point A?

A. \(-13\)

B. \(-3\)

C. \(-2\)

D. A and B

15- Which of the following shows the numbers in increasing order?

A. \(\frac{3}{13}, \frac{4}{11}, \frac{5}{14}, \frac{2}{5}\)

B. \(\frac{3}{13}, \frac{5}{14}, \frac{4}{11}, \frac{2}{5}\)

C. \(\frac{3}{13}, \frac{5}{14}, \frac{2}{5}, \frac{4}{11}\)

D. \(\frac{5}{14}, \frac{3}{13}, \frac{2}{5}, \frac{4}{11}\)

16- If \(x=- 4\), which of the following equations is true?

A. \(x(3x-1)=50\)

B. \(5(11-x^2 )=-25\)

C. \(3(-2x+5)=49\)

D. \(x(-5x-19)=-3\)

17- What is the missing prime factor of number 450?
\(450=2^1×3^2×…\) _________

18- What is the perimeter of the following shape? (it’s a right triangle)

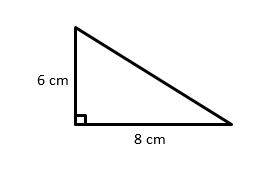
A. 14 cm

B. 18 cm

C. 24 cm

D. 32 cm

19- 65 is what percent of 50?

A. \(50 \%\)

B. \(77 \%\)

C. \(130 \%\)

D. \(140 \%\)

20- Which of the following expressions has a value of \(-23\)?

A. \(-10+(-8)+ \frac{5}{2}×(-2)\)

B. \(5×3+(-2)×18\)

C. \(-10+6×8÷(-4)\)

D. \((-3) × (-7) + 2\)

Best 6th Grade MCAS Math Workbook Resource for 2024

Answers:

2- C
\(2205÷315=\frac{2205}{315}=\frac{441}{63}=\frac{147}{21}= 7\)

3- B
\(112=22+x \)
Subtract 22 from both sides of the equation. Then:
\(x=112-22=90\)

4- D
Distance that car B travels \(=1.2 ×\) distance that car A travels
=\(1.2×221.5=265.8 \) km

5- D
The perimeter of the trapezoid is 38.
Therefore, the missing side (height) is \(= 38 – 8 – 10 – 11 = 9\)
Area of the trapezoid: \(A = \frac{1}{2} h (b_1 + b_2) = \frac{1}{2}1 (9) (8 + 10) = 81\)

6- D
A. \(3^1+12=3+12=15\)
B. \(3^3-3^2=27-9=18\)
C. \(3^4-60=81-60=21\)
D. \(3^5-218=243-218=25\)

7- B
Alfred has \(x\) apple which is 15 apples more than the number of apples Alvin owns. Therefore:
\(x-15=40→x=40+15=55\)
Alfred has 55 apples.
Let \(y\) be the number of apples that Baron has. Then: \(y=\frac{1}{5}×55=11\)

8- A
Complementary angles add up to 180 degrees.
\( β+150^\circ=180^\circ→β=180^\circ-150^\circ=30^\circ\)
The sum of all angles in a triangle is 180 degrees. Then:
\(α+β+50^\circ=180^\circ→α+30^\circ+50^\circ=180^\circ\)
\(→α+80^\circ=180^\circ→α=180^\circ-80^\circ=100^\circ\)

9- C
Let \(x\) be the original price.
If the price of a laptop is decreased by \(15\%\) to $425, then:
\(85 \% \space of \space x=425⇒ 0.85x=425 ⇒ x=425÷0.85=500\)

10- C
Let \(x\) and \(y\) be two sides of the shape. Then:
\(x+1=1+1+1→x=2\)
\(y+6+2=5+4→y+8=9→y=1\)
Then, the perimeter is:
\(1+5+1+4+1+2+1+6+2+1=24\)

11- B
First, put the numbers in order from least to greatest: \(1, 1, 1, 2, 3, 3, 3, 4, 5, 6, 6\)
The Mode of the set of numbers is: 1 and 3 (the most frequent numbers)
Median is: 3 (the number in the middle)

12- C
\(x×92=x×(90+2)=(x×90)+(x×2)\)

13- C
The ratio of pens to pencils is \(3 : 5\). Therefore there are 3 pens out of all 8 pens and pencils. To find the answer, first dived 96 by 8 then multiply the result by 3.
\(96÷8=12→12×3=36\)
There are 36 pens and 60 pencils \((96-36)\). Therefore, 24 more pens should be put in the box to make the ratio \(1 : 1\)

14- D
If the value of point A is greater than the value of point B, then the distance of two points on the number line is: the value of A- the value of B
A. \(-\frac{24}{3}-(-13)=-8+13=5=5\)
B. \(-3-(-\frac{24}{3})=-3+8=5=5\)
C. \(-2-(-\frac{24}{3})=-2+8=6≠5\)

15- B
\(\frac{3}{13}≅0.23 , \frac{5}{14}≅0.357 , \frac{4}{11}≅0.36 , \frac{2}{5}=0.4\)

16- B
Plugin the value of \(x\) in the equations. \(x = -4\), then:
A.\(x(3x-1)=50→-4(3(-4)-1)=-4(-12-1)=-4(-13)=52≠50\)
B. \(5(11-x^2 )=-25→5(11-(-4)^2 )= 5(11-16)=5(-5)=-25\)
C. \(3(-2x+5)=49→3(-2(-4)+5)=3(8+5)=39≠49\)
D. \(x(-5x-19)=-3→-4(-5(-4)-19=-4(20-19)=-4≠-3\)

17- 5
Let \(x\) be the missing prime factor of 450.
\(450= 2 × 3 × 3 × x ⇒ x =\frac{450}{18} ⇒ x = 25=5×5\)

18- C
Use the Pythagorean theorem to find the hypotenuse of the triangle.
\(a^2+b^2=c^2→6^2+8^2=c^2→36+64=c^2→100=c^2→c=10\)
The perimeter of the triangle is: \(6+8+10=24\)

19- C
Use the percent formula:
\(Part = \frac{percent}{100} × whole\)
\(65= \frac{percent}{100} × 50⇒ 65 = \frac{percent ×50}{100}⇒ 65=\frac{percent ×5}{10}\)
multiply both sides by 10.
\(650 =percent ×5, \space divide \space both \space sides \space by \space 5.\)
130 = percent
The answer is \(130\%\)

20- A
Let’s check the options provided.
A. \(-10+(-8)+ (\frac{5}{2})×(-2)=-10+(-8)+(-5)=-10-13=-23\)
B. \(5×3+(-2)×18=15+(-38)=-21\)
C. \(-10+6×8÷(-4)=-10+48÷(-4)=-10-12=-22\)
D. \((-3)× (-7)+ 2=21+2=23\)

Looking for the best resource to help you succeed on the Grade 6 MCAS Math test?

The Most Comprehensive Review for 6th-Grade Students