How to Find the Perimeter of Right-Angled Triangle?

The perimeter of a right triangle is the sum of the lengths of all three sides, including the hypotenuse, height, and base.

Related Topics

• How to Solve Pythagorean Theorem Problems?

A step-by-step guide to finding the perimeter of the right-angled triangle

The perimeter of a right triangle is the sum of its sides. For example, if \(a, b\), and \(c\) are sides of a right-angled triangle, its perimeter would be: \((a + b + c)\). Now that the triangle is right-angled, we can say that its perimeter is the sum of the lengths of the two sides and the hypotenuse.

How to find the perimeter of a right triangle?

There are several ways to find the perimeter of a right triangle. We must check the parameters according to the given conditions to do this. Let’s see the different methods.

Method 1:

If the lengths of the sides are not given but the right triangle is drawn to scale, we use a ruler to measure the sides and add the dimensions of each side. The perimeter of the right-angled triangle is:

Perimeter \(\color{blue}{= sum\:of\:all\:the\:sides\:measured\:by\:the\:ruler}\)

Method 2:

Knowing the length of all sides of a right triangle is enough to add their length. For example, if \(p, q,\) and \(r\) are the given sides, then:

Perimeter \(\color{blue}{= p + q + r}\)

This method is only possible if the measurement of all sides is known.

Method 3: 

When both sides of a right triangle are given, we first find the missing side using the Pythagorean theorem and then calculate the perimeter of the right triangle. Pythagoras’s theorem states that the square of the hypotenuse length equals the sum of the squares of the other two sides of the right triangle.

\(\left(Hypotenuse\right)^2\:=\:\left(Base\right)^2\:+\:\left(Height\right)^2\)

See the triangle below, where \(a\) and \(b\) are sides that make a \(90°\) angle together, and \(c\) is the hypotenuse. For this purpose, the Pythagorean theorem is written as follows:

\(c^2\:=\:a^2\:+\:b^2\)

Finding the Perimeter of the Right-Angled Triangle – Example 1:

If the base is \(5\) units and the hypotenuse is \(13\) units, find the perimeter of a right triangle.

Solution:

Use the Pythagorean theorem to find the height:

\(\left(Hypotenuse\right)^2\:=\:\left(Base\right)^2\:+\:\left(Height\right)^2\)

\(\left(13\right)^2=\left(5\right)^2+\left(a\right)^2\)

\(\left(13\right)^2-\left(5\right)^2=\left(a\right)^2\)

\(169-25=144\)

\(a=\sqrt{144}=12\)

Height \(= 12\) units

The perimeter of the right triangle \(= 5 + 13 + 12 = 30\) units.

Exercises for Finding the Perimeter of the Right-Angled Triangle

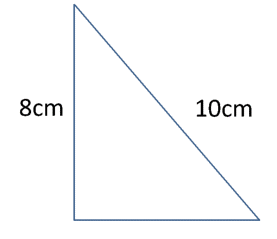
Find the perimeter of each Right-Angled Triangle.

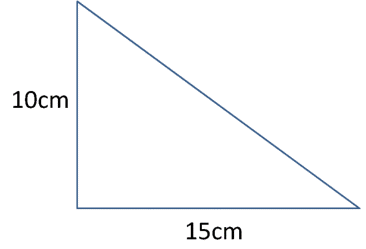
1. \(\color{blue}{43\space cm}\)
2. \(\color{blue}{24\space cm}\)