How to Solve Parallel Lines and Transversals Problems? (+FREE Worksheet!)

When a line (transversal) intersects two parallel lines in the same plane, eight angles are formed. In this article, we will teach you how to find the missing angles in this case by using the Parallel Lines and Transversals rules.

Related Topics

• Special Right Triangles
• How to Solve Triangles Problems
• How to Find Volume and Surface Area of Cubes
• How to Calculate Cylinder Volume and Surface Area
• How to Find Complementary and Supplementary Angles

A step-by-step guide to solving Parallel Lines and Transversals Problem

• When a line (transversal) intersects two parallel lines in the same plane, eight angles are formed. In the following diagram, a transversal intersects two parallel lines. Angles 1, 3, 5, and 7 are congruent. Angles 2, 4, 6, and 8 are also congruent.
• In the following diagram, the following angles are supplementary angles (their sum is 180):

• Angles 1 and 8
• Angles 2 and 7
• Angles 3 and 6
• Angles 4 and 5

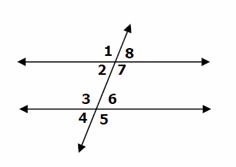
Examples

Parallel Lines and Transversals – Example 1:

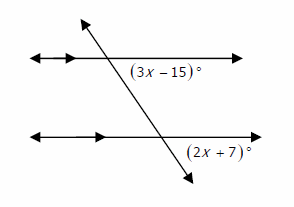
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?

Solution:

The two angles \(3x-15\) and \(2x+7\) are equivalent.
That is: \(3x-15=2x+7\)
Now, solve for \(x: 3x-15+15=2x+7+15 →\)
\(3x=2x+22→3x-2x=2x+22-2x→x=22\)

Parallel Lines and Transversals – Example 2:

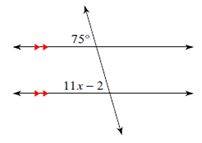
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?

Solution:

The two angles \(75^\circ\) and \(11x-2\) are equal. \(11x-2=75\)
Now, solve for \(x: 11x-2+2=75+2→ 11x=77→x=\frac{77}{11}→x=7\)

Parallel Lines and Transversals – Example 3:

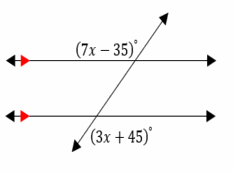
In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?

Solution:

The two angles \(7x-35\) and \(3x+45\) are equivalents.
That is: \(7x-35=3x+45\)
Now, solve for \(x: 7x-35+35=3x+45+35 →\)
\(7x=3x+80→7x-3x=3x+80-3x→4x=80→x=\frac{80}{4}→x=20\)

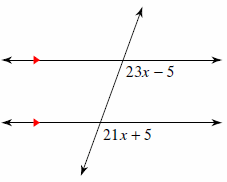
Parallel Lines and Transversals – Example 4:

In the following diagram, two parallel lines are cut by a transversal. What is the value of \(x\)?

Solution:

The two angles \(3x-27\) and \(-x+33\) are equivalents.
That is: \(3x-27=-x+33\)
Now, solve for \(x: 3x-27+27=-x+33+27 →\)
\(3x=-x+60→3x+x=-x+60+x→4x=60→x=\frac{60}{4}→x=15\)

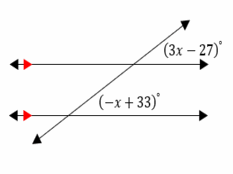
Exercises for Parallel Lines and Transversals

Find missing angles with Parallel Lines and Transversals.

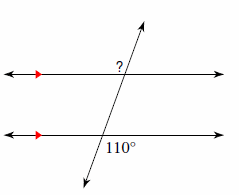
1.Find the measure of the angle indicated.

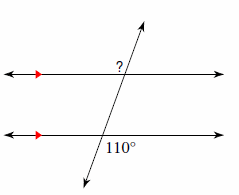
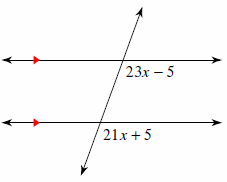
2. Solve for \(x\).

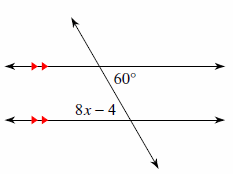
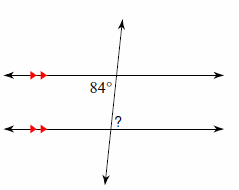
3. Find the measure of the angle indicated.

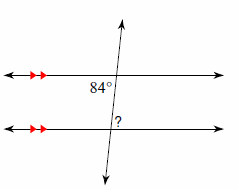
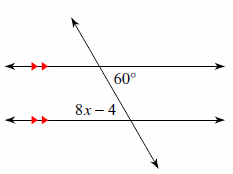
4. Solve for \(x\).

1.\(\color{blue}{110^\circ}\)

2.\(\color{blue}{x=8}\)

3. \(\color{blue}{84^\circ}\)

4.\(\color{blue}{x=5}\)