Parallel, Perpendicular, and Intersecting Lines

A sequence of points linked via a straight path is described as being a line. 

Lines are typically characterized by \(2\) points. They may be indicated with \(1\) letter in the lower case or via \(2\) capital letters. 

A line doesn’t have any thickness and can be extended forever in each direction. A line’s length is not defined and it may include infinite quantities of points. See the subsequent figure to understand how lines and points differ.

Kinds of Lines

Simply like the various kinds of points, there are also distinct kinds of lines that you can easily distinguish based on their distinctive properties.

• Horizontal Lines – Lines mapped from left-to-right or right-to-left and which are parallel to the \(x\)-axis in a plane are known as horizontal lines.
• Vertical Lines – Lines mapped from up to down or down to up and are parallel to the \(y\)-axis in a plane are known as vertical lines.
• Intersecting Lines – Whenever \(2\) lines cross one another and meet up at a point, they’re called intersecting lines. The point where they meet up is called the point of intersection.

 Intersecting Lines Properties

The subsequent points show the characteristics of intersecting lines that assist us in identifying them with ease.

• Intersecting lines link at a single point, and they can’t meet up at more than a single point.
• Intersecting lines meet up with one another at any angle that’s bigger than \(0°\) and lower than \(180°\).

• Perpendicular Lines– Whenever \(2\) lines intersect precisely at \(90°\), they’re called perpendicular lines.
• Parallel Lines –\(2\) lines are understood to be parallel if they don’t intersect at any point as well as they are equidistant.

Non-intersecting Lines Properties

The subsequent points show the characteristics of non-intersecting lines that assist us in identifying them with ease.

• non-intersecting lines don’t ever meet up and they don’t share any kind of common point. They’re additionally called parallel lines.
• The gap in-between non-intersecting lines is constantly equal.
• The size of any common perpendicular drawn in between the \(2\) non-intersecting lines is constantly equal.

Hints on Points and Lines

• Whenever \(2\) distinct points are linked they create a line.
• A line goes in two directions forever.
• Parallel lines don’t intersect one another.
• The line which intersects with one another at \(90°\) are called perpendicular lines.
• \(2\) or more points that lie on one straight line are called collinear points.

Parallel, Perpendicular, and Intersecting Lines – Example 1:

State whether the given pair of lines are parallel, perpendicular, or intersecting.

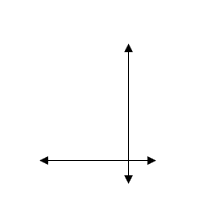
Solution:

These two lines cross each other and intersect at \(90°\) so they are both intersecting and perpendicular to each other.

Parallel, Perpendicular, and Intersecting Lines – Example 2:

State whether the given pair of lines are parallel, perpendicular, or intersecting.

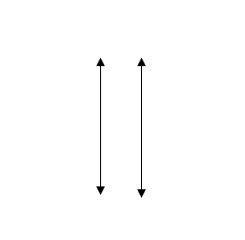
Solution:

These two lines do not intersect at any point so they are parallel.

Exercises for Parallel, Perpendicular, and Intersecting Lines

1)

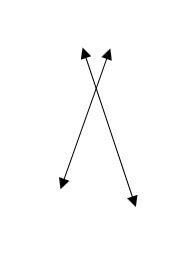
2)

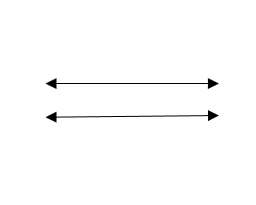
Answers

1. \(\color{blue}{Intersecting}\)
2. \(\color{blue}{Parallel}\)