Applying Floor And Ceiling Functions: Practical Examples And Solutions
The absolute value depicts a number’s distance from zero, essential in complex numbers and error analysis. Ceiling functions round up to the nearest integer, while floor functions round down, crucial in algorithms and discrete mathematics. Together, they streamline numerical methods and optimize computer algorithms. For education statistics and research, visit the National Center for Education Statistics.
[include_netrun_products_block from-products="product/ged-math-workbook-comprehensive-math-practices-and-solutions-the-ultimate-test-prep-book-with-two-full-length-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"] [include_netrun_products_block from-products="product/ged-math-workbook-comprehensive-math-practices-and-solutions-the-ultimate-test-prep-book-with-two-full-length-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Absolute value function:
\( “|…|” \) is the symbol of “absolute value” in mathematics. This function returns the absolute value of a number, meaning if it is positive, the function returns the number unchanged, and if it’s negative, the function multiplies the number in \( -1 \). For education statistics and research, visit the National Center for Education Statistics.
For example: For education statistics and research, visit the National Center for Education Statistics.
\( |-3|=3 \) , \( |-e|=e \)
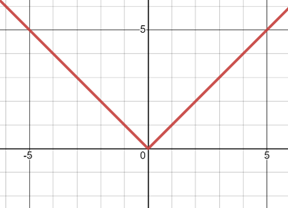
So in general form, \( |x|=x \) for \(x≥0 \) and \( |x|=-x for x<0\). The graph of absolute value function, looks like the letter “V”:
Floor function:
Brackets, or brackets without the bent tops \( “⌊…⌋” \) are the mathematical symbol for floor function. This function rounds the number inside it down to the nearest integer. Meaning if you have a positive number with decimals, it omits the decimal and returns the integer that remains. And if the number is negative, it omits the decimal and also subtracts the result by \( 1\), thus rounding it down, since more negative means a smaller number.
For example:
\( ⌊3.3⌋=3, ⌊ 6.01⌋=6, ⌊ -2.1⌋=-3, ⌊ e⌋=2 , ⌊ -e⌋=-3 , ⌊-π⌋=-4 \)
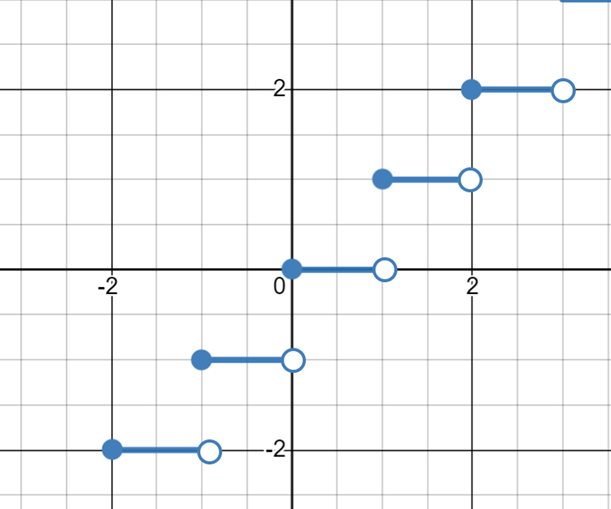
The graph of floor function looks like steps. This is because for all values between two integers, the functions result would be one of those integers.
The empty circles indicate that the functions result, is not the same as where the empty circles are. For example, at \(1\) itself, the answer is no longer zero and is \( 1\) instead. This wasn’t the case at,
For example:
\( 0.999999 \)
Ceiling function:
This function is denoted using \( “⌈…⌉” \) symbol, or brackets without the bent bottoms. It is the opposite of floor function, and rounds numbers up to their next integer. So if you have a positive number, the ceiling function returns its next integer. And if you have a negative number, the function removes the decimal and returns what’s left (basically next integer, meaning the bigger number. This can be a bit confusing in negative numbers).
For example:
\(⌈2.1⌉=3 , ⌈5.02⌉=6 , ⌈-5.02⌉=-5, ⌈e⌉=3 , ⌈-e⌉=-2 , ⌈π⌉=4 \)
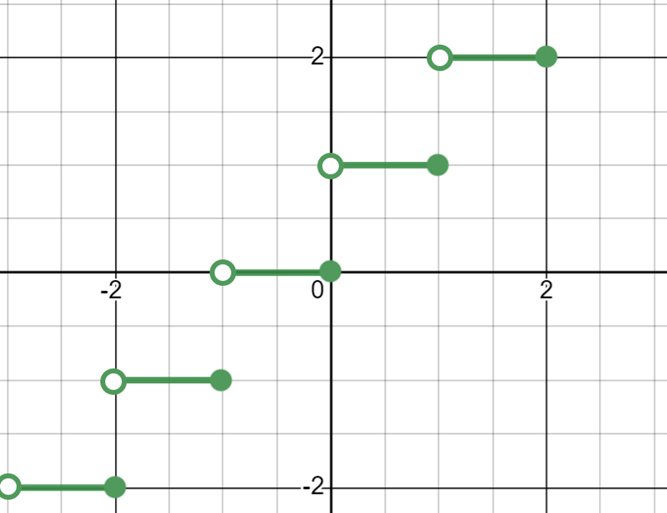
The graph of ceiling function, also looks like steps. Compared to floor function, it is shifted to left by 1 unit, and switched the placement of filled and empty circles.
Related to This Article
More math articles
- Top 10 7th Grade PARCC Math Practice Questions
- 8th Grade STAAR Math Worksheets: FREE & Printable
- 4th Grade Mathematics Worksheets: FREE & Printable
- Deciphering Change: Differential Equations in Daily Life
- How to Find the y-Intercept of a Line?
- Full-Length ALEKS Math Practice Test
- 10 Most Common 7th Grade PARCC Math Questions
- Full-Length CLEP College Algebra Practice Test-Answers and Explanations
- Free GED Math Worksheets [Updated for 2026]
- FREE TASC Math Practice Test
What people say about "Applying Floor And Ceiling Functions: Practical Examples And Solutions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.